Đề kiểm tra 45 phút - Đề số 2 - Chương 2 - Đại số 7

Đề bài

Bài 1: Một lớp có 35 học sinh giỏi, khá và trung bình. Số học sinh giỏi và số học sinh khá tỉ lệ thuận với  2 và 3, số học sinh khá và số học sinh trung bình tỉ lệ thuận với 4 và 5. Tính số học sinh giỏi, khá và trung bình.

Bài 2: Có 5 người cùng làm một công việc trong 6 ngày. Hỏi nếu có 15 người( với cùng năng suất) thì hoàn thành công việc trong mấy ngày? 

Bài 3: Cho hàm số \(y = f(x) = 2x\). 

a) Tính \(f\left( {{3 \over 2}} \right);f\left( {{1 \over 2}} \right).\)

b) Tìm x biết \(f(x) = -5.\)

c) Vẽ đồ thị của hàm số và cho biết điểm \(M(-3;-1)\) có thuộc đồ thị của hàm số hay không?

LG bài 1

Phương pháp giải:

Sử dụng tính chất dãy tỉ số bằng nhau \(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{{a + c + e}}{{b + d + f}}\)

Lời giải chi tiết:

Gọi x, y, z, là số học sinh giỏi, khá, trung bình.

Vì có 35 học sinh nên \(x+y+z=35\) 

Theo tính chất dãy tỉ số bằng nhau, ta có:

\( {x \over 8} = {y \over {12}} = {z \over {15}} = {{x + y + z} \over {8 + 12 + 15}} = {{35} \over {35}} = 1  \)

\(\Rightarrow x = 8;y = 12;z = 15. \)

Vậy lớp có 8 học sinh giỏi; 12 học sinh khá; 15 học sinh trung bình.

LG bài 2

Phương pháp giải:

Sử dụng tính chất hai đại lượng tỉ lệ nghịch: 

Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia.

\( \dfrac{x_{1}}{x_{2}}= \dfrac{y_{2}}{y_{1}}; \dfrac{x_{1}}{x_{3}}= \dfrac{y_{3}}{y_{1}}\); ...

Lời giải chi tiết:

Đặt x là số người làm và y là số ngày để họ hoàn thành công việc.

Ta có bảng tóm tắt sau: 

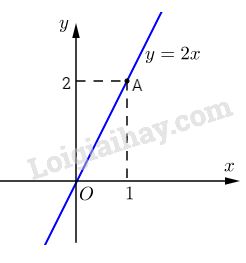
Vì x, y là hai đại lượng tỉ lệ nghịch nên ta có :

\({{{x_1}} \over {{x_2}}} = {{{y_2}} \over {{y_1}}} \Rightarrow {5 \over {15}} = {{{y_2}} \over 6} \Rightarrow {y_2} = {{5.6} \over {15}} = 2\)

Vậy 15 người làm trong 2 ngày.

LG bài 3

Phương pháp giải:

Thay \(x=x_0\) vào hàm số \(y=f(x)\) để tìm \(f(x_0)\)

Đồ thị hàm số \(y = ax (a ≠ 0)\) là đường thẳng đi qua gốc toạ độ và \(A(1;a)\)

Điểm \(M(x_0;y_0)\) thuộc đồ thị hàm số \(y=ax\) nếu \(y_0=ax_0\)

Lời giải chi tiết:

a) Ta có: \(f\left( {{3 \over 2}} \right) = 2.{3 \over 2} = 3;\)

              \(f\left( { - {1 \over 2}} \right) = 2.\left( { - {1 \over 2}} \right) =  - 1\)

b) \(f\left( x \right) =  - 5 \Rightarrow 2x =  - 5 \Rightarrow x =  - {5 \over 2}\)

c) Đồ thị của hàm số \(y = 2x\) là đường thẳng qua O và điểm \(A(1 ;2)\) (xem hình vẽ).

Vì \(2.( - 3) \ne  - 1\) nên \(M(-3 ;-1)\) không thuộc đồ thị của hàm số \(y = 2x.\)

Loigiaihay.com