Đề kiểm tra 45 phút (1 tiết) – Chương 1 – Đề số 1 – Đại số và giải tích 11Đáp án và lời giải chi tiết Đề thi kiểm tra 45 phút (1 tiết) – Chương 1 – Đề số 1 – Đại số và giải tích 11 Quảng cáo
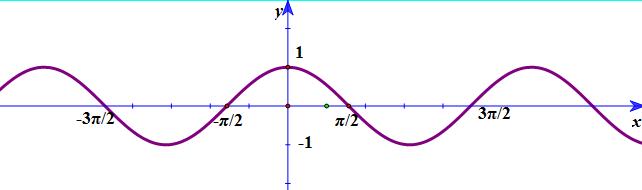
Đề bài I. PHẦN TRẮC NGHIỆM Câu 1: Với những giá trị nào của \(x\) thì giá trị của các hàm số tương ứng sau bằng nhau \(y = \tan 3x\) và \(\tan (\dfrac{\pi }{3} - 2x)\) A. \(x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{5},\,k \in \mathbb{Z}\) B. \(x = \dfrac{\pi }{{15}} + k\pi ,\,k \in \mathbb{Z}\) C. \(x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{2},\,k \in \mathbb{Z}\) D. \(x = \dfrac{\pi }{5} + k\dfrac{\pi }{5},\,k \in \mathbb{Z}\) Câu 2: Tìm m để phương trình \(\dfrac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}} = m\) có nghiệm. A. \( - 3 \le m \le 2\) B. \(m > 2\) C. \(m \ge - 3\) D. \(\dfrac{2}{{11}} \le m \le 2\) Câu 3: Nghiệm của phương trình \(\sin x + \sqrt 3 \cos x = \sqrt 2 \) là: A. \(x = - \dfrac{\pi }{{12}} + k2\pi ,\;x = \dfrac{{5\pi }}{{12}} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\) B. \(x = - \dfrac{\pi }{4} + k2\pi ,\;x = \dfrac{{3\pi }}{4} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\) C. \(x = \dfrac{\pi }{3} + k2\pi ,\;x = \dfrac{{2\pi }}{3} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\) D. \(x = - \dfrac{\pi }{4} + k2\pi ,\;x = - \dfrac{{5\pi }}{4} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\) Câu 4 : Chọn mệnh đề đúng: A. Hàm số \(y = \sin x\) có chu kỳ \(T = \pi \) B. Hàm số \(y = \cos x\) và hàm số \(y = \tan x\) có cùng chu kỳ. C. Hàm số \(y = \cot x\) và hàm số \(y = \tan x\) có cùng chu kỳ. D. Hàm số \(y = \cot x\) có chu kỳ \(T = 2\pi \) Câu 5: Nghiệm dương bé nhất của phương trình \(2{\sin ^2}x + 5\sin x - 3 = 0\) là: A. \(x = \dfrac{\pi }{3}.\) B. \(x = \dfrac{\pi }{{12}}.\) C. \(x = \dfrac{\pi }{6}.\) D. \(x = \dfrac{{5\pi }}{6}.\) Câu 6: Hàm số nào sau đây có đồ thị không là đường hình sin? A. \(y = \sin x\) B. \(y = \cos x\) C. \(y = \sin 2x\) D. \(y = \cot x\) Câu 7: Tập xác định của hàm số\(y = f(x) = 2\cot (2x - \dfrac{\pi }{3}) + 1\) là: A. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}\) B. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\) C. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + k\pi ,k \in \mathbb{Z}} \right\}\) D. \(\mathbb{R}\backslash \left\{ {\dfrac{{5\pi }}{{12}} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\) Câu 8: Nghiệm của phương trình \(\tan (x - \dfrac{\pi }{2}) = \sqrt 3 \) là: A. \(x = \dfrac{{5\pi }}{6} + k\pi \). B. \(x = \dfrac{{5\pi }}{6} + k2\pi \). C. \(x = \dfrac{\pi }{6} + k2\pi \). D. \(x = \dfrac{\pi }{6} + k\pi \). Câu 9: Tập nghiệm của phương trình \(\cos 3x = - 1\) là: A. \(\left\{ { - \dfrac{\pi }{2} + k2\pi |k \in \mathbb{Z}} \right\}.\) B. \(\left\{ {\pi + k2\pi |k \in \mathbb{Z}} \right\}.\) C. \(\left\{ {\dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}|k \in \mathbb{Z}} \right\}.\) D. \(\left\{ {\dfrac{{k2\pi }}{3}|k \in \mathbb{Z}} \right\}.\) Câu 10: Trong các hàm số sau, hàm số nào là hàm số chẵn. A. \(y = \sin \left| {2016x} \right| + c{\rm{os}}2017x\). B. \(y = 2016\cos x + 2017\sin x\). C. \(y = \cot 2015x - 2016\sin x\). D. \(y = \tan 2016x + \cot 2017x\). Câu 11: Nghiệm của phương trình \(\sin 2x = \dfrac{{\sqrt 2 }}{2}\) là: A.\(\,x = \dfrac{\pi }{8} + k2\pi ;x = \dfrac{{3\pi }}{8} + k2\pi (k \in Z)\) B. \(\,x = \dfrac{\pi }{4} + k2\pi ;x = \dfrac{{3\pi }}{4} + k2\pi \,(k \in Z)\) C. \(\,x = \dfrac{\pi }{4} + k\pi ;x = \dfrac{{3\pi }}{4} + k\pi (k \in Z)\) D. \(\,x = \dfrac{\pi }{8} + k\pi ;x = \dfrac{{3\pi }}{8} + k\pi ;k \in Z)\) Câu 12: Giá trị nhỏ nhất m của hàm số \(y = 3\sin x + 1\) là. A. m = 4 B. m = -2 C. m = 3 D. m = 1 Câu 13: Tập xác định của hàm số \(y = f(x) = \dfrac{1}{{\sqrt {1 - sinx} }}\) A. \(\mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\) B. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\) C. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\) D. \(\phi \) Câu 14: Giá trị nhỏ nhất của hàm số \(y = {\sin ^2}x - 4\sin x - 5\) là: A. -9 B. 0 C. 9 D. -8 Câu 15: Đồ thị hàm số nào dưới đây nhận trục tung làm trục đối xứng? A. \(y = \sin x - \cos x\). B. \(y = 2\sin x\). C. \(y = 2\sin \left( { - x} \right)\). D. \(y = - 2\cos x\) Câu 16: Nghiệm của phương trình \(2{\sin ^2}x + \sin x\cos x - 3{\cos ^2}x = 0\) là: A. \(x = \dfrac{\pi }{4} + k\pi \); \(x = \arctan ( - \dfrac{3}{2}) + k\pi ,k \in \mathbb{Z}\) B. \(x = \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}\) C. \(x = \dfrac{\pi }{4} + k\pi \);\(x = \arctan ( - 3) + k\pi ,k \in \mathbb{Z}\) D. \(x = \arctan ( - \dfrac{3}{2}) + k\pi ,k \in \mathbb{Z}\) Câu 17: Phương trình lượng giác nào dưới đây có nghiệm là: \(x = \dfrac{\pi }{6} + k\pi ,k \in \mathbb{Z}.\) A. \(\cos 2x = \dfrac{{\sqrt 3 }}{2}.\) B. \(\cot x = \sqrt 3 .\) C. \(\tan x = \sqrt 3 .\) D. \(\sin \left( {x - \dfrac{\pi }{3}} \right) = - \dfrac{1}{2}\) Câu 18: Giá trị lớn nhất M của hàm số \(y = \sin x + \cos x\) là. A. \(M = 2\) B. \(M = 2\sqrt 2 \) C. \(M = 1\) D. \(M = \sqrt 2 \) Câu 19: Nghiệm của phương trình \(\sin x = \cos x\) là: A. \(x = \dfrac{\pi }{4} + k2\pi \). B. \(x = \dfrac{\pi }{4} + k\pi \). C. \(x = \dfrac{\pi }{4}\). D. \(x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\). Câu 20: Đồ thì hình bên là đồ thị của hàm số nào?
A. \(y = \sin x\) B. \(y = \cot x\) C. \(y = \tan x\) D. \(y = \cos x\) II. PHẦN TỰ LUẬN Câu 21: Giải các phương trình sau a) \(\sin 3x - \cos 2x = 0\) b) \(\dfrac{{\sin x + \sqrt 3 \cos x}}{{\sin x - \cos \dfrac{\pi }{4}}} = 0\) Câu 22: Giải phương trình : \(2{\cos ^2}\left( {\dfrac{\pi }{4} - 2x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1\) Lời giải chi tiết I. PHẦN TRẮC NGHIỆM
Câu 1: Ta có: \(\tan 3x = \tan (\dfrac{\pi }{3} - 2x) \)\(\Leftrightarrow 3x = \dfrac{\pi }{3} - 2x + k\pi \;\left( {k \in \mathbb{Z}} \right)\) \( \Leftrightarrow 5x = \dfrac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\) \( \Leftrightarrow x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{5}\;\left( {k \in \mathbb{Z}} \right)\) Chọn đáp án A. Câu 2: Ta có: \(\dfrac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}} = m \) \(\Leftrightarrow \cos x + 2\sin x + 3 = m\left( {2\cos x - \sin x + 4} \right)\) \( \Leftrightarrow \left( {2m - 1} \right)\cos x - \left( {m + 2} \right)\sin x = 3 - 4m\) Điều kiện có nghiệm: \({\left( {2m - 1} \right)^2} + {\left( {m + 2} \right)^2} \ge {\left( {3 - 4m} \right)^2}\) \( \Leftrightarrow 4{m^2} - 4m + 1 + {m^2} + 4m + 4\)\( \ge 9 - 24m + 16{m^2}\) \( \Leftrightarrow 11{m^2} - 24m + 4 \le 0 \)\(\Leftrightarrow \dfrac{2}{{11}} \le m \le 2.\) Chọn đáp án D. Câu 3: Ta có:\(\sin x + \sqrt 3 \cos x = \sqrt 2 \) \(\begin{array}{l} \( \Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 2 }}{2}\) \( \Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = \sin \dfrac{\pi }{4} \)\( \Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{3} = \dfrac{\pi }{4} + k2\pi \\x + \dfrac{\pi }{3} = \pi - \dfrac{\pi }{4} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\) \( \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{{12}} + k2\pi \\x = \dfrac{{5\pi }}{{12}} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\) Chọn đáp án A. Câu 4: + Hàm số \(y = \sin x,\,y = \cos x\) có chu kỳ là \(T = 2\pi \) + Hàm số \(y = \tan x,y = \cot x\) có chu kì là \(T = \pi \) Chọn đáp án C. Câu 5: Ta có: \(2{\sin ^2}x + 5\sin x - 3 = 0 \)\(\Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sin x + 3} \right) = 0\) \( \Leftrightarrow \sin x = \dfrac{1}{2} \)\(\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\) Nghiệm dương bé nhất của phương trình là \(x = \dfrac{\pi }{6}.\) Chọn đáp án C. Câu 6: Hàm số \(y = \cot x\) có đồ thị không là đường hình sin. Chọn đáp án D. Câu 7: \(y = f(x) = 2\cot (2x - \dfrac{\pi }{3}) + 1 \)\(= \dfrac{{2\cos (2x - \dfrac{\pi }{3})}}{{\sin (2x - \dfrac{\pi }{3})}} + 1\) ĐKXĐ: \(\sin \left( {2x - \dfrac{\pi }{3}} \right) \ne 0 \) \(\Leftrightarrow \left( {2x - \dfrac{\pi }{3}} \right) \ne k\pi \;\left( {k \in \mathbb{Z}} \right)\) \( \Leftrightarrow x \ne \dfrac{\pi }{6} + k\dfrac{\pi }{2}\;\left( {k \in \mathbb{Z}} \right)\) Câu 8: Ta có: \(\tan (x - \dfrac{\pi }{2}) = \sqrt 3 \) \(\Leftrightarrow \tan (x - \dfrac{\pi }{2}) = \tan \dfrac{\pi }{3}\) \( \Leftrightarrow x - \dfrac{\pi }{2} = \dfrac{\pi }{3} + k\pi \;\left( {k \in \mathbb{Z}} \right)\) \( \Leftrightarrow x = \dfrac{{5\pi }}{6} + k\pi \;\left( {k \in \mathbb{Z}} \right)\) Chọn đáp án A. Câu 9: Ta có: \(\cos 3x = - 1 \Leftrightarrow 3x = \pi + k2\pi \,\left( {k \in \mathbb{Z}} \right)\) \( \Leftrightarrow x = \dfrac{\pi }{3} + k\dfrac{{2\pi }}{3}\;\left( {k \in \mathbb{Z}} \right)\) Chọn đáp án C. Câu 10: Đáp án A: TXĐ: D=R. Ta có: \(\begin{array}{l} Hàm số \(y = \sin \left| {2016x} \right| + c{\rm{os}}2017x\) là hàm số chẵn. Chọn đáp án A. Câu 11: Ta có: \(\sin 2x = \dfrac{{\sqrt 2 }}{2} \Leftrightarrow \sin 2x = \sin \dfrac{\pi }{4}\) \( \Leftrightarrow \left[ \begin{array}{l}2x = \dfrac{\pi }{4} + k2\pi \\2x = \pi - \dfrac{\pi }{4} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\) \(\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{8} + k\pi \\x = \dfrac{{3\pi }}{8} + k\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\) Chọn đáp án D. Câu 12: Ta có: \(\sin x \in \left[ { - 1;1} \right] \) \(\begin{array}{l} Chọn đáp án B. Câu 13: Ta có: \(\sin x \in \left[ { - 1;1} \right] \Rightarrow 1 - \sin x \in \left[ {0;2} \right]\) Điều kiện xác định: \(1 - \sin x \ne 0 \Leftrightarrow \sin x \ne 1 \) \(\Leftrightarrow x \ne \dfrac{\pi }{2} + k2\pi \;\left( {k \in \mathbb{Z}} \right)\) Chọn đáp án C. Câu 14: Ta có: \(y = {\sin ^2}x - 4\sin x - 5 \)\(= \left( {{{\sin }^2}x - 4\sin x + 4} \right) - 9 \)\(= {\left( {\sin x - 2} \right)^2} - 9\) + \(\sin x \in \left[ { - 1;1} \right] \Rightarrow \sin x - 2 \in \left[ { - 3; - 1} \right] \) \(\Leftrightarrow {\left( {\sin x - 2} \right)^2} \in \left[ {1;9} \right]\) Khi đó \(y \ge 1 - 9 = - 8\) Chọn đáp án D. Câu 15: Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng, do đó ta kiểm tra hàm số chẵn ở mỗi đáp án. Dễ thấy hàm số \(y = - 2\cos x\) là hàm chẵn nên nhận trục tung làm trục đối xứng. Chọn đáp án D. Câu 16: Ta có: \(2{\sin ^2}x + \sin x\cos x - 3{\cos ^2}x = 0 \) \(\Leftrightarrow \left( {\sin x - \cos x} \right)\left( {2\sin x + 3\cos x} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}\sin x = \cos x\\2\sin x = - 3\cos x\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}\tan x = 1\\\tan x = - \dfrac{3}{2}\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{4} + k\pi \\x = \arctan \left( { - \dfrac{3}{2}} \right) + k\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\) Chọn đáp án A. Câu 17: Ta có: \(\cot x = \sqrt 3 \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \;\left( {k \in \mathbb{Z}} \right)\) Chọn đáp án B. Câu 18: Ta có: \(y = \sin x + \cos x = \sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right) \) \(\begin{array}{l} \(\Rightarrow y \in \left[ { - \sqrt 2 ;\sqrt 2 } \right]\) Chọn đáp án D. Câu 19: Ta có: \(\sin x = \cos x \Leftrightarrow \tan x = 1 \) \(\Leftrightarrow x = \dfrac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\) Chọn đáp án B. Câu 20: Đồ thị hình bên là của hàm số \(y = \cos x\) Chọn đáp án D. II. PHẦN TỰ LUẬN Câu 21: \(a) \sin 3x - \cos 2x = 0 \Leftrightarrow \sin 3x = \cos 2x \)\(\Leftrightarrow \sin 3x = \sin \left( {\dfrac{\pi }{2} - 2x} \right)\) \(\begin{array}{l} \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{\pi }{{10}} + k\dfrac{{2\pi }}{5}}\\{x = \dfrac{\pi }{2} + k2\pi }\end{array}} \right.\) Vậy phương trình có nghiệm: \(x = \dfrac{\pi }{{10}} + k\dfrac{{2\pi }}{5};\,\,x = \dfrac{\pi }{2} + k2\pi \)\(\) \(b) \dfrac{{\sin x + \sqrt 3 \cos x}}{{\sin x - \cos \dfrac{\pi }{4}}} = 0 \, (1)\) ĐK: \(\sin x - \cos \dfrac{\pi }{4} \ne 0\) \(\begin{array}{l} \(\begin{array}{l}(1) \Leftrightarrow \sin x + \sqrt 3 \cos x = 0 \\\Leftrightarrow \dfrac{1}{2}\sin x + \dfrac{{\sqrt 3 }}{2}\cos x = 0 \\\Leftrightarrow \cos \dfrac{\pi }{3}\sin x + \sin \dfrac{\pi }{3}\cos x = 0\\ \Leftrightarrow \sin (x + \dfrac{\pi }{3}) = 0 \Leftrightarrow x + \frac{\pi }{3} = k\pi \\ \Leftrightarrow x = \dfrac{{ - \pi }}{3} + k\pi \end{array}\) Kết hợp với điều kiện (*) ta thấy thỏa mãn. Vậy phương trình có nghiệm: \(x = \dfrac{{ - \pi }}{3} + k\pi \) Câu 22: \(2{\cos ^2}\left( {\dfrac{\pi }{4} - 2x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1\) \( \Leftrightarrow 1 + \cos \left( {\dfrac{\pi }{2} - 4x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1\)\(\Leftrightarrow \sin 4x + \sqrt 3 \cos 4x = 2\left( {2{{\cos }^2}x - 1} \right)\) \(\begin{array}{l} \Leftrightarrow \dfrac{1}{2}\sin 4x + \dfrac{{\sqrt 3 }}{2}\cos 4x = \cos 2x \\\Leftrightarrow \sin \dfrac{\pi }{6}\sin 4x + \cos \dfrac{\pi }{6}\cos 4x = \cos 2x\\ \Leftrightarrow \cos \left( {4x - \dfrac{\pi }{6}} \right) = \cos 2x \end{array}\) \(\begin{array}{l} \(\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{\pi }{{12}} + k\pi }\\{x = \dfrac{\pi }{{36}} + k\dfrac{\pi }{3}}\end{array}} \right.\,\,(k \in \mathbb{Z})\) Vậy phương trình có nghiệm là: \(x = \dfrac{\pi }{{12}} + k\pi ;\,x = \dfrac{\pi }{{36}} + k\dfrac{\pi }{3}\) Loigiaihay.com
|




















Danh sách bình luận