Đề kiểm tra 15 phút - Đề số 9 - Bài 6 - Chương 2 - Hình học 9

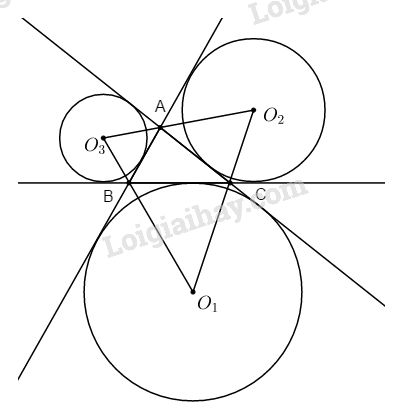
Đề bài

Cho tam giác ABC. Gọi O₁, O₂, O₃ là tâm các đường tròn bàng tiếp cỉa tam giác ABC. Chứng minh rằng A, B, C là chân các đường cao của tam giác O₁O₂O₃.

Lời giải chi tiết

Ta có các tia CO₁ và CO₂ là phân giác của góc ngoài ở đỉnh C của ∆ABC nên C nằm trên đường thẳng O₁O₂ và \(\widehat {{O_1}CB} = \widehat {{O_2}CA}\) (1)

Vì CO₃ là tia phân giác của \(\widehat {BCA}\) nên

\(\widehat {BC{O_3}} = \widehat {AC{O_3}}\) (2)

Từ (1) và (2) ta có: \(\widehat {{O_1}C{O_3}} = \widehat {{O_3}C{O_2}} = 90^\circ \)  hay CO₃ là đường cao của tam giác O₁O₂O₃.

Chứng minh tương tự AO₁, BO₂ cũng là các đường cao của tam giác O₁O₂O₃.

Loigiaihay.com