Đề kiểm tra 15 phút - Đề số 9 - Bài 4, 5 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 9 - Bài 4, 5 - Chương 1 - Hình học 8 Quảng cáo
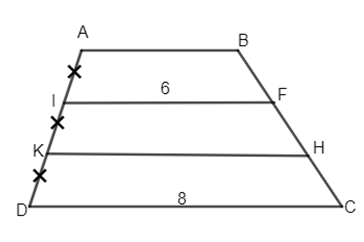
Đề bài Cho hình thang ABCD \(\left( {AB// CD} \right)\) . Trên cạnh AD lấy hai điểm I và K sao cho AI = IK = KD. Từ I và K kẻ các đường thẳng song song với hai đáy cắt BC theo thứ tự tại F và H. a) Chứng minh: BF = FH = HC. b) Cho CD = 8cm; IF = 6cm. Tính AB và HK. Phương pháp giải - Xem chi tiết - Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. - Định lí: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai. - Định lí: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy. Lời giải chi tiết
a) Theo đề bài ta có: \(AB//IF//KH//DC\) Suy ra ABHK; IFCD là các hình thang. Xét hình thang ABHK có I là trung điểm AK (gt) và IF//AB//HK \( \Rightarrow IF\) là đường trung bình của hình thang ABHK \( \Rightarrow F\) là trung điểm của HB hay BF = FH. Xét hình thang IFCD có K là trung điểm ID (gt) và HK//IF//DC \( \Rightarrow KH\) là đường trung bình của hình thang IFCD Suy ra \(FH = HC\) Do đó \( BF = FH = HC.\) b) Do KH là đường trung bình của hình thang IFCD nên \(KH = \dfrac{{IF + CD} }{2} = \dfrac{{6 + 8} }{ 2} = 7\left( {cm} \right).\) Trong hình thang ABHK, IF là đường trung bình: \(IF = \dfrac{{AB + HK} }{ 2} \Rightarrow 2IF = AB + 7\) \( \Rightarrow 2.6 = AB + 7 \Rightarrow AB = 5(cm).\) Loigiaihay.com
|




















Danh sách bình luận