Đề kiểm tra 15 phút - Đề số 3 - Bài 5 - Chương 2 - Hình học 9

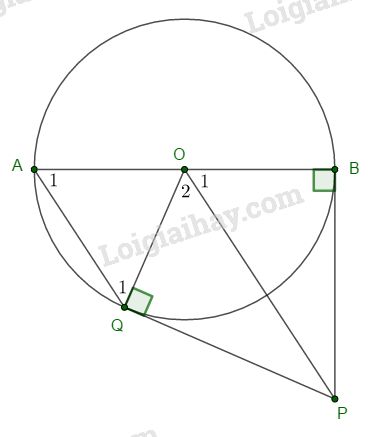
Đề bài

Cho đường tròn tâm O, đường kính AB. Kẻ tiếp tuyến tại B với đường tròn (O), trên tiếp tuyến lấy P. Qua A kẻ đường thẳng song song với OP cắt (O) tại Q. Chứng minh PQ là tiếp tuyến của đường tròn (O).

Lời giải chi tiết

Ta có: AQ // OP (gt)

\(\left\{ {\matrix{   {{{\widehat A}_1} = {{\widehat O}_1}\,\left( \text{cặp góc đồng vị} \right)}  \cr   {{{\widehat Q}_1} = {{\widehat O}_2}\,\left( \text{cặp góc so le trong} \right)}  \cr  } } \right.\)

mà \({\widehat A_1} = {\widehat Q_1}\) (∆AOQ cân) \( \Rightarrow {\widehat O_1} = {\widehat O_2}\)

Xét \(∆PQO\) và \(∆PBO\) có:

OP chung

\({\widehat O_1} = {\widehat O_2}\) (cmt)

\(OQ = OB (=R)\)

Vậy \(∆PQO = ∆PBO\) (c.g.c) \( \Rightarrow \widehat {PQO} = \widehat {PBO} = 90^o\)

Hay \(PQ ⊥ OQ\), chứng tỏ PQ là tiếp tuyến của (O).

 Loigiaihay.com