Đề kiểm tra 15 phút - Đề số 8 - Bài 4 - Chương 3 - Hình học 9

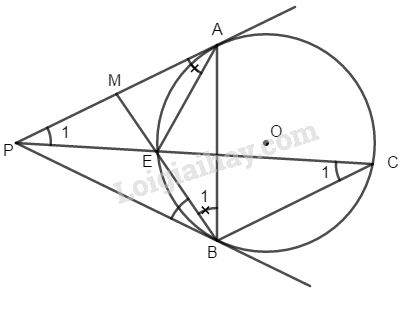
Đề bài

Từ điểm P bên ngoài đường tròn (O, kẻ hai tiếp tuyến PA và PB đến (O). Đường thẳng song song với PA kẻ từ B cắt (O) tại C, PC cắt đường tròn (O) tại điểm thứ hai là E. Đường BE cắt PA tại M.

a) Chứng minh: \(PM^2= BM.ME\)

b) Chứng minh rằng M là trung điểm của PA.

Lời giải chi tiết

a) PA // BC \(\Rightarrow \widehat {{C_1}} = \widehat {{P_1}}\) ( so le trong)

\(\widehat {{C_1}} = \widehat {MBP}\) ( góc nội tiếp bằng góc giữa tiếp tuyến và một dây cùng chắn cung BE)

Do đó \(∆PME\) và \(∆BMP\) đồng dạng (g.g)

\(\Rightarrow\dfrac{{PM}}{{BM}} = \dfrac{{ME} }{ {PM}}\)

\(\Rightarrow PM^2= BM.ME\)            (1)

b) Tương tự ta có hai tam giác AME và BMA đồng dạng (g.g) vì có :

\(\widehat {MAE} = \widehat {{B_1}}\) và \(\widehat {AMB}\) chung

\( \Rightarrow \dfrac{{AM}}{{BM}} =\dfrac {{ME}}{{AM}}\)

\(\Rightarrow  AM^2 = BM.ME\)  (2)

Từ (1) và (2) \( \Rightarrow P{M^2} = A{M^2}\)

\( \Rightarrow  PM = AM\) hay M là trung điểm của PA.

 Loigiaihay.com