Đề kiểm tra 15 phút - Đề số 4 - Bài 7 - Chương 3 - Hình học 9

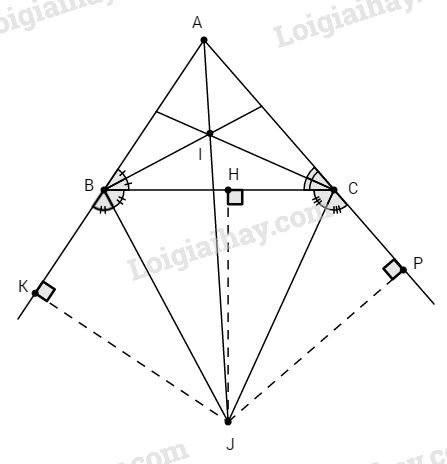
Đề bài

Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác trong của hai góc B và C và J là giao điểm các phân giác ngoài của hai góc đó.

a) Chứng minh BICJ là tứ giác nội tiếp.

b) Chứng minh rằng ba điểm A, I, J thẳng hàng.

Lời giải chi tiết

 

a) Ta có BI và BJ là phân giác của hai góc kề bù nên \(BI \bot BJ\) hay \(\widehat {IBJ} = 90^\circ .\)

Tương tự \(\widehat {{\rm{ICJ}}} = 90^\circ \)

\( \Rightarrow \widehat {IBJ} + \widehat {{\rm{ICJ}}} = 180^\circ \)

\( \Rightarrow \) Tứ giác BICJ nội tiếp.

b) Hạ JH, JK, JP lần lượt vuông góc với BC, AB, AC ta có :

\(JH = JK\) ( tính chất phân giác)

\(JH = JP\) ( tính chất phân giác)

\( \Rightarrow  JK = JP\) chứng tỏ J thuộc phân giác góc A.

Do đó ba điểm A, I, J thẳng hàng.

Loigiaihay.com