Đề kiểm tra 15 phút - Đề số 4 - Bài 3 - Chương 2 - Đại số 9

Đề bài

Bài 1. Viết phương trình đường thẳng (d) đi qua hai điểm A(0; -3) và B(1; -1)

Bài 2. Cho hai đường thẳng d₁ : \(y = mx + m + 2\) và d₂ : \(y = -x\). Tìm m để d₁ và d₂ song song.

Bài 3. Cho hàm số \(y = {4 \over 3}x + 4\)

a. Vẽ đồ thị hàm số

b. Tìm tọa độ giao điểm A, B của đồ thị lần lượt với Ox và Oy. Tính diện tích tam giác OAB (đơn vị đo trên các trục tọa độ là xăng-ti-mét).

LG bài 1

Phương pháp giải:

Gọi phương trình đường thẳng d có dạng: \(y = ax + b\) 

Thay tọa độ các điểm A và B vào phương trình \(y = ax + b\) để tìm a, b.

Lời giải chi tiết:

Phương trình đường thẳng d có dạng: \(y = ax + b\) 

Do \(A(0;-3) \in \left( d \right) \Rightarrow  - 3 = a.0 + b\)\( \Rightarrow b =  - 3.\)

Khi đó : \(y = ax – 3\)

Do \(B(1;-1) \in \left( d \right) \Rightarrow  - 1 = a.1 - 3\)\( \Rightarrow a = 2\)

Vậy phương trình của d là : \(y = 2x – 3\)

LG bài 2

Phương pháp giải:

Hai đường thẳng \(y = ax + b\) và \(y = a'x + b'\) song song với nhau khi và chỉ khi \(a = a', b ≠ b'\).

Lời giải chi tiết:

Để d₁ // d₂ 

\(\Leftrightarrow \left\{ {\matrix{   {m =  - 1}  \cr   {m + 2 \ne 0}  \cr  } } \right. \Leftrightarrow m =  - 1\)

LG bài 3

Phương pháp giải:

Cách vẽ đồ thị của hàm số \(y = ax + b (a ≠ 0).\) 

- Chọn điểm \(P(0; b)\) (trên trục \(Oy\)). 

- Chọn điểm \(Q\left( { - \dfrac{b}{a};0} \right)\) (trên trục \(Ox\)).

- Kẻ đường thẳng \(PQ\) ta được đồ thị của hàm số \(y=ax+b.\)

Lời giải chi tiết:

a. Bảng giá trị:

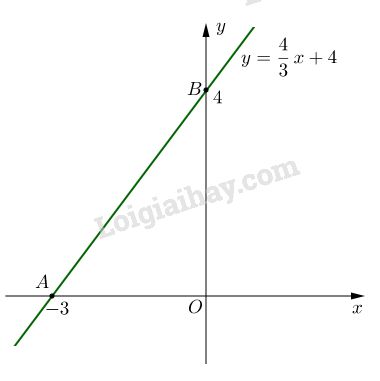
Đồ thị của hàm số \(y = {4 \over 3}x + 4\) là đường thẳng qua hai điểm \(A(-3; 0)\) và \(B(0;4)\)

b. Ta có: \(A(-3; 0)\) và \(B(0; 4)\) lần lượt là giao điểm của đồ thị với trục Ox và Oy

\( \Rightarrow OA = \left| { - 3} \right| = 3\) và \(OB = 4\). 

Diện tích \(S_{\Delta OAB} = {1 \over 2}.OA.OB = {1 \over 2}.3.4 = 6\)\(\,\left( {c{m^2}} \right)\)

Loigiaihay.com