Đề kiểm tra 15 phút - Đề số 1 - Bài 4 - Chương 3 - Hình học 9

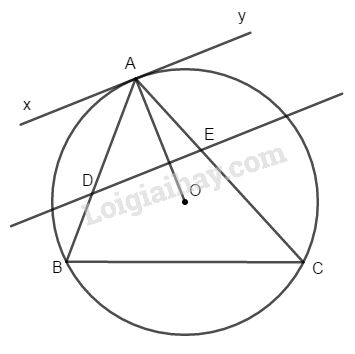
Đề bài

Cho ∆ABC nội tiếp đường tròn (O). Một đường thẳng song song với tiếp tuyến tại A của đường tròn (O) cắt các cạnh AB, AC lần lượt ở D và E. Chứng tỏ ∆ABC và ∆ADE đồng dạng và \(AB.AD = AC.AE.\)

Lời giải chi tiết

Ta có : DE // xAy

\(\Rightarrow \widehat {xAD} = \widehat {ADE}\) ( so le trong)

Lại có \(\widehat {xAD} = \widehat {BCA}\) ( góc giữa tiếp tuyến và một dây bằng góc nội tiếp cùng chắn cung AB) => \(\widehat {ADE} = \widehat {BCA}\).

Xét \(∆ABC\) và \(∆ADE\) có:

+) \(\widehat {BAC}\) chung

+) \(\widehat {ADE} = \widehat {BCA}\)

Do đó \(∆ABC\) đồng dạng \(∆AED\) (g.g)

\(\Rightarrow \dfrac{{AB}}{ {AC}} = \dfrac{{AE} }{ {AD}}\)

\(\Rightarrow AB.AD = AC.AE.\)

 Loigiaihay.com