Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 2 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 2 - Hình học 9 Quảng cáo
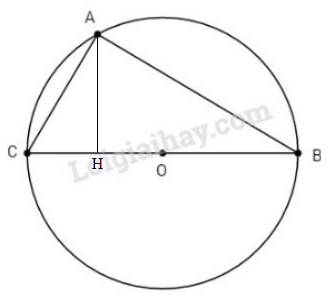
Đề bài Cho đường tròn đường kính BC cố định và \(BC = 2R.\) Lấy điểm A di động trên đường tròn (A khác B và C). a. Chứng minh rằng ∆ABC là tam giác vuông b. Chứng minh rằng : \({S_{ABC}} \le {R^2}.\) Phương pháp giải - Xem chi tiết Sử dụng: Trong một tam giác, đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác đó là tam giác vuông Diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng Lời giải chi tiết a. Ta có: \(OA = OB = OC (= R)\) \( \Rightarrow OA = {{BC} \over 2}\) Trong ∆ABC, AO là đường trung tuyến và \(AO = {{BC} \over 2}\) nên ∆ABC vuông tại A. b. Kẻ đường cao AH của tam giác ABC. Ta có: \({S_{ABC}} = {1 \over 2}BC.AH \)\(\;= {1 \over 2}.2R.AH = R.AH\) Trong tam giác vuông AHO, ta có: \(AH ≤ AO\) (cạnh góc vuông < cạnh huyền) hay \(AH ≤ R\) \( \Rightarrow AH.R \le {R^{2.}}\) Vậy \({S_{ABC}} \le {R^2}\) Dấu “=” xảy ra khi A trùng với các đầu mút của đường kính vuông góc với BC. Chú ý : Từ kết quả trên bạn có thể xét bài toán : “Tìm vị trí của điểm A để diện tích ∆ABC lớn nhất”. Loigiaihay.com
|




















Danh sách bình luận