Câu hỏi:
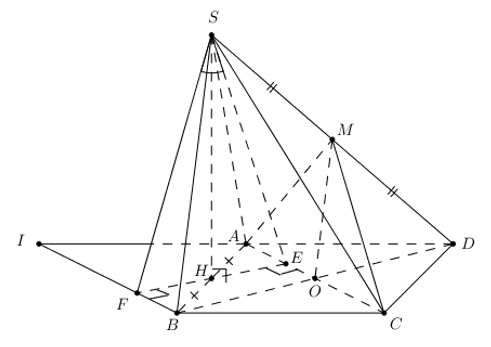
Chóp S.ABCD, \(\left( SAB \right)\bot \left( ABCD \right),\,\,\Delta SAB\) đều, \(ABCD\) là hình vuông, \(AB=a\). M là trung điểm của SD. Tính \(\widehat{\left( \left( MAC \right);\left( SAC \right) \right)}\).
- A \(\arccos \frac{5}{7}\)
- B \(\arccos \frac{5}{9}\)
- C \(\arccos \frac{1}{7}\)
- D \(\arccos \frac{1}{5}\)
Phương pháp giải:
Lời giải chi tiết:
* Phương pháp thay thế góc
* Qua B vẽ d // AC, \(d\cap AD=I\). Nối \(AC\cap BD=O,\,\,\Delta SBD\) có OM là đường trung bình \(\Rightarrow \left\{ \begin{align} OM//SB \\ BI//AC \\ \end{align} \right.\)
\(\Rightarrow \left( MAC \right)//\left( SBI \right)\Rightarrow \widehat{\left( \left( MAC \right);\left( SAC \right) \right)}=\widehat{\left( \left( SBI \right);\left( SAC \right) \right)}\)
* Vẽ \(SH\bot AB\Rightarrow SH\bot \left( ABCD \right).\) Vẽ \(HE\bot AC;\,\,HF\bot IB\Rightarrow \left\{ \begin{align} SE\bot AC \\ SF\bot IB \\ \end{align} \right.\).
\(\Rightarrow \widehat{\left( \left( SBI \right);\left( SAC \right) \right)}=\widehat{ESF}\) (cá biệt 2).
* \(HE=BO=\frac{a}{\sqrt{2}},\,\,HE=\frac{a}{2\sqrt{2}}\)
* Tam giác vuông SHE : \(SE=\sqrt{\frac{3{{a}^{2}}}{4}+\frac{{{a}^{2}}}{8}}=\frac{a\sqrt{7}}{\sqrt{8}}=\frac{a\sqrt{7}}{2\sqrt{2}}\)
* \(\cos \widehat{ESF}=\frac{E{{F}^{2}}-S{{E}^{2}}-S{{F}^{2}}}{-2SE.SF}=\frac{\frac{{{a}^{2}}}{2}-\frac{7{{a}^{2}}}{8}-\frac{7{{a}^{2}}}{8}}{-2.\frac{7{{a}^{2}}}{8}}=\frac{5}{7}\)
Chọn đáp án A.