20 bài tập hai mặt phẳng vuông góc mức độ vận dụng caoLàm bàiQuảng cáo
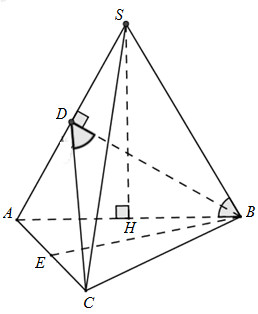
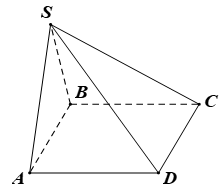
Câu hỏi 1 : Cho khối chóp S.ABC có đáy là tam giác ABC vuông cân tại B có \(AB = BC = 4\). Gọi H là trung điểm của AB, \(SH \bot \left( {ABC} \right)\). Mặt phẳng \(\left( {SBC} \right)\) tạo với đáy một góc \({60^0}\). Cosin góc giữa 2 mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SAB} \right)\) là:
Đáp án: C Phương pháp giải: +) Xác định góc giữa mặt phẳng (SBC) và mặt đáy bằng cách xác định hai đường thẳng lần lượt thuộc hai mặt và cùng vuông góc với giao tuyến BC. +) Gọi D là trung điểm của SA. +) Chứng minh \(BD \bot SA\) bằng cách chứng minh tam giác SAB đều. +) Chứng minh \(CD \bot SA\) bằng cách chứng minh tam giác SCA cân tại C. +) Chứng minh \( \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SAC} \right)} \right)} = \widehat {\left( {CD;BD} \right)}\) +) Áp dụng định lí Cosin trong tam giác. Lời giải chi tiết:
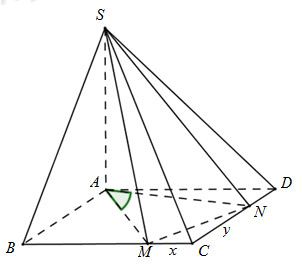
Ta có: \(\left. \begin{array}{l}BC \bot AB\\BC \bot SH\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\) \(\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\SB \bot BC\\AB \bot BC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {60^0}\) Lại có: H là trung điểm của AB mà \(SH \bot AB\) nên tam giác SAB cân tại S có góc SBA = 600 nên \( \Rightarrow \Delta SAB\) đều. Gọi D là trung điểm của SA \( \Rightarrow BD \bot SA\) \(\left( {SAC} \right) \cap \left( {SAB} \right) = SA\) Ta có: \(\begin{array}{l}BD = \frac{{4\sqrt 3 }}{2} = 2\sqrt 3 ;SD = AD = \frac{1}{2}SA = \frac{1}{2}AB = 2;\\AC = 4\sqrt 2 ;SC = \sqrt {S{B^2} + B{C^2}} = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \end{array}\) \( \Rightarrow \Delta SAC\) cân tại C \( \Rightarrow CD \bot SA\) \(\left. \begin{array}{l}\left( {SAC} \right) \cap \left( {SAB} \right) = SA\\CD \bot SA\\BD \bot SA\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SAC} \right)} \right)} = \widehat {\left( {CD;BD} \right)}\) Ta có:\(CD = \sqrt {A{C^2} - A{D^2}} = \sqrt {32 - 4} = 2\sqrt 7 \)\( \Rightarrow cos\widehat {BDC} = \dfrac{{B{D^2} + C{D^2} - B{C^2}}}{{2.BD.CD}} = \dfrac{{12 + 28 - 16}}{{2.2\sqrt 3 .2\sqrt 7 }} = \dfrac{{\sqrt 3 }}{{\sqrt 7 }}\) Chọn C. Câu hỏi 2 : Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Hai điểm M, N lần lượt thay đổi trên cạnh CB và CD, đặt CM = x, CN = y. Tìm hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SAN) tạo với nhau một góc \({90^0}\)?
Đáp án: A Phương pháp giải: +) Xác định góc giữa (SAM) và (SAN) bằng cách xác định hai đường thẳng lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến SA. +) Sử dụng định lí Pytago tính các đoạn thẳng AM, AN, MN theo a, x, y. +) Áp dụng định lí Pytago đảo chứng minh tam giác AMN vuông. Lời giải chi tiết:
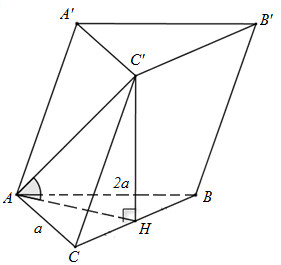
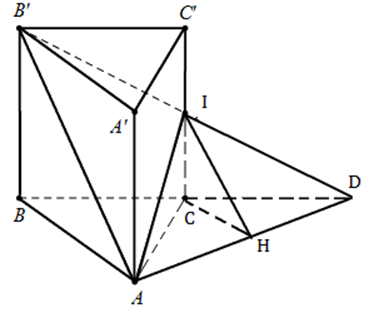
\(\begin{array}{l}\left. \begin{array}{l}\left( {SAM} \right) \cap \left( {SAN} \right) = SA\\AM \bot SA\\AN \bot SA\end{array} \right\}\\ \Rightarrow \widehat {\left( {\left( {SAM} \right);\left( {SAN} \right)} \right)} = \widehat {\left( {AM;AN} \right)} = \widehat {MAN} = {90^0}\end{array}\) Ta có: \(\begin{array}{l}A{M^2} = A{B^2} + B{M^2} = {a^2} + {\left( {a - x} \right)^2}\\A{N^2} = A{D^2} + D{N^2} = {a^2} + {\left( {a - y} \right)^2}\\M{N^2} = {x^2} + {y^2}\end{array}\) Xét tam giác vuông AMN có: \(\begin{array}{l}M{N^2} = A{M^2} + A{N^2}\\ \Rightarrow {x^2} + {y^2} = {a^2} + {\left( {a - x} \right)^2} + {a^2} + {\left( {a - y} \right)^2}\\ \Leftrightarrow 0 = 4{a^2} - 2ax - 2ay\\ \Leftrightarrow x + y = 2a\end{array}\) Chọn A. Câu hỏi 3 : Cho hình lăng trụ \(ABC.A'B'C'\) có \(AB = 2a,AC = a,AA' = \dfrac{{a\sqrt {10} }}{2},\widehat {BAC} = {120^0}.\) Hình chiếu vuông góc của \(C'\)lên mặt phẳng \(\left( {ABC} \right)\) là trung điểmcủa cạnh BC. Tính số đo góc giữa hai mặt phẳng (ABC) và \(\left( {ACC'A'} \right)\) ?
Đáp án: C Phương pháp giải: +) Áp dụng định lí Cosin trong tam giác tính HC. +) Áp dụng định lí Pytago đảo chứng minh \(HA \bot CA\) +) Chứng minh \(\widehat {\left( {\left( {ABC} \right);\left( {ACC'A'} \right)} \right)} = \widehat {\left( {AH;AC'} \right)}\) +) Sử dụng định lí Pytago tính C’H. Chứng minh tam giác C’AH vuông cân. Lời giải chi tiết:
Gọi H là trung điểm của BC. Theo giả thiết ta có: \(C'H \bot \left( {ABC} \right)\) Xét tam giác ABC có: \(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.cos\widehat {BAC} = 4{a^2} + {a^2} - 2.2a.a.\left( { - \dfrac{1}{2}} \right) = 7{a^2} \Rightarrow BC = a\sqrt 7 \Rightarrow HC = \dfrac{{a\sqrt 7 }}{2}\\cos\widehat {ACB} = \dfrac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}} = \dfrac{{{a^2} + 7{a^2} - 4{a^2}}}{{2.a.a\sqrt 7 }} = \dfrac{2}{{\sqrt 7 }}\\ \Rightarrow A{H^2} = A{C^2} + H{C^2} - 2AC.HC.cos\widehat {ACH} = {a^2} + \dfrac{7}{4}{a^2} - 2.a.\dfrac{{a\sqrt 7 }}{2}.\dfrac{2}{{\sqrt 7 }} = \dfrac{{3{a^2}}}{4} \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2}\end{array}\) Ta có: \(A{H^2} + A{C^2} = \dfrac{{3{a^2}}}{4} + {a^2} = \dfrac{{7{a^2}}}{4} = H{C^2}\) \(\Delta ACH\)vuông tại A (Định lý Pi – ta – go đảo) \( \Rightarrow HA \bot CA\) Vì \(C'H \bot \left( {ABC} \right) \Rightarrow C'H \bot AC\) \( \Rightarrow AC \bot \left( {AHC'} \right) \Rightarrow AC \bot AC'\)
Ta có: \(\left. \begin{array}{l}\left( {ABC} \right) \cap \left( {ACC'A'} \right) = AC\\AH \bot AC\\AC' \bot AC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {ABC} \right);\left( {ACC'A'} \right)} \right)} = \widehat {\left( {AH;AC'} \right)} = \widehat {C'AH}\) (Vì \(C'H \bot \left( {ABC} \right) \Rightarrow C'H \bot AH \Rightarrow \Delta C'HA\) vuông tại H \( \Rightarrow \widehat {C'AH} < {90^0}\)) \(C'H \bot \left( {ABC} \right) \Rightarrow C'H \bot BC\) Xét tam giác vuông \(CC'H\)có: \(C'H = \sqrt {CC{'^2} - H{C^2}} = \sqrt {\dfrac{{10{a^2}}}{4} - \dfrac{{7{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow C'H = AH \Rightarrow \Delta C'AH\) vuông cân tại H \( \Rightarrow \widehat {C'AH} = {45^0}\) Chọn C. Câu hỏi 4 : Cho hình chóp \(S.ABC\) có đáy \(\widehat{BAC}={{90}^{0}},\,\,\,BC=2a,\,\,\,\widehat{ACB}={{30}^{0}}.\) Mặt phẳng \(\left( SAB \right)\) vuông góc với mặt phẳng \(\left( ABC \right).\) Biết rằng tam giác \(SAB\) cân tại \(S\) và tam giác \(SBC\) vuông tại \(S.\) Tính diện tích tam giác \(SAB.\)
Đáp án: C Phương pháp giải: Sử dụng các định lí về hai mặt phẳng vuông góc Lời giải chi tiết:
Gọi \(H\) là trung điểm của \(AB,\) tam giác \(SAB\) cân tại \(S\Rightarrow SH\bot AB.\) Mà \(\left( SAB \right)\bot \left( ABC \right)\) nên \(SH\bot \left( ABC \right)\) và đặt \(SH=x.\) Tam giác \(ABC\) vuông tại có \(\left\{ \begin{array}{l}AB = BC.\sin C = a\\AC = BC.\cos C = a\sqrt 3 \end{array} \right..\) Ta có \(SB=\sqrt{S{{H}^{2}}+H{{B}^{2}}}=\sqrt{{{x}^{2}}+\frac{{{a}^{2}}}{4}},\) \(HC=\sqrt{H{{A}^{2}}+A{{C}^{2}}}=\frac{a\sqrt{13}}{2}\) Và \(SC=\sqrt{S{{H}^{2}}+H{{C}^{2}}}=\sqrt{{{x}^{2}}+\frac{13{{a}^{2}}}{4}}\) Tam giác SBC vuông tại S nên \(S{{B}^{2}}+S{{C}^{2}}=B{{C}^{2}}\) \(\Leftrightarrow {{x}^{2}}+\frac{{{a}^{2}}}{4}+{{x}^{2}}+\frac{13\,{{a}^{2}}}{4}=4{{a}^{2}}\Leftrightarrow {{x}^{2}}=\frac{{{a}^{2}}}{4}\)\(\Leftrightarrow x=\frac{a}{2}\Rightarrow SH=\frac{a}{2}.\) Vậy diện tích tam giác \(SAB\) là \({{S}_{\Delta \,SAB}}=\frac{1}{2}.SH.AB=\frac{{{a}^{2}}}{4}.\) Chọn C
Câu hỏi 5 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A,\,\,\,AB=a.\) Tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy. Đường thẳng \(BC\) tạo với mặt phẳng \(\left( SAC \right)\) góc \({{30}^{0}}.\) Tính diện tích tam giác \(ABC.\)
Đáp án: A Phương pháp giải: Sử dụng các định lí về hai mặt phẳng vuông góc Lời giải chi tiết:
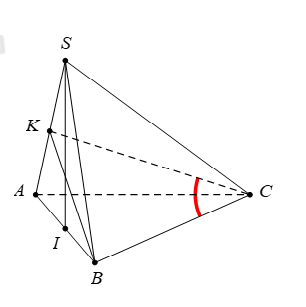
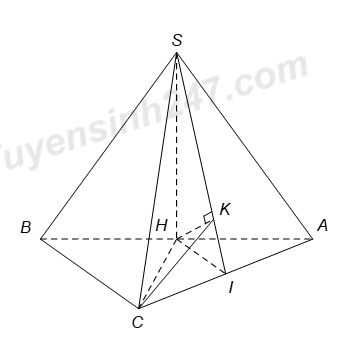
Gọi \(I\) là trung điểm của \(AB,\) tam giác \(SAB\) đều \( \Rightarrow \,\,\left\{ \begin{array}{l}SI = \frac{{a\sqrt 3 }}{2}\\SI \bot AB\end{array} \right.\) Mà \(\left( {SAB} \right) \bot \left( {ABC} \right)\)\(\Rightarrow \) \(SI \bot \left( {ABC} \right)\); \(\left\{ \begin{array}{l}SI \bot AC\\AB \bot AC\end{array} \right. \Rightarrow AC \bot \left( {SAB} \right).\) Kẻ \(BK\) vuông góc với \(SA\) tại \(K,\) ta có \(BK=\frac{a\sqrt{3}}{2},\,\,\,BK\bot \left( SAC \right).\) Do đó, góc giữa \(BC\) và \(mp\,\,\left( SAC \right)\) là \(\widehat{BCK}\,\,\Rightarrow \,\,\widehat{BCK}={{30}^{0}}.\) Khi đó \(BC=\frac{BK}{\sin \widehat{BCK}}=a\sqrt{3}\Rightarrow AC=\sqrt{B{{C}^{2}}-A{{B}^{2}}}=a\sqrt{2}.\) Vậy diện tích tam giác \(ABC\) là \({{S}_{\Delta \,ABC}}=\frac{1}{2}.AB.AC=\frac{{{a}^{2}}\sqrt{2}}{2}.\) Chọn A Câu hỏi 6 : Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(C\). Gọi \(H\) là trung điểm \(AB\). Biết rằng \(SH\) vuông góc với mặt phẳng \(\left( ABC \right)\) và \(AB=SH=a.\) Tính cosin của góc \(\alpha \) tọa bởi hai mặt phẳng \(\left( SAB \right)\) và \(\left( SAC \right)\).
Đáp án: D Phương pháp giải: Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông Lời giải chi tiết:
Ta có \(SH\bot \left( ABC \right)\Rightarrow SH\bot CH\). (1) Tam giác ABC cân tại C nên \(CH\bot AB\). (2) Từ (1) và (2), suy ra \(CH\bot \left( SAB \right)\). Gọi I là trung điểm \(AC\)\(\Rightarrow \,\,HI//BC\xrightarrow{BC\,\bot \,\,AC}HI\bot AC\). (3) Mặt khác \(AC\bot SH\) (do \(SH\bot \left( ABC \right)\)). (4) Từ (3) và (4), suy ra \(AC\bot \left( SHI \right)\). Kẻ \(HK\bot SI\text{ }\,\left( K\in SI \right)\). (5) Từ \(AC\bot \left( SHI \right)\Rightarrow AC\bot HK\). (6). Từ (5) và (6), suy ra \(HK\bot \left( SAC \right)\). Vì \(\left\{ \begin{array}{l}HK \bot \left( {SAC} \right)\\HC \bot \left( {SAB} \right)\end{array} \right.\) nên góc giữa hai mặt phẳng \(\left( SAC \right)\) và \(\left( SAB \right)\) bằng góc giữa hai đường thẳng \(HK\) và \(HC\). Ta có \(HK\bot \left( SAC \right)\Rightarrow HK\bot CK\Rightarrow \Delta CHK\( vuông tại K. Có \(CH=\frac{1}{2}AB=\frac{a}{2}\); \(\frac{1}{H{{K}^{2}}}=\frac{1}{S{{H}^{2}}}+\frac{1}{H{{I}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{\left( \frac{1}{2}.\frac{a}{\sqrt{2}} \right)}^{2}}}\Rightarrow HK=\frac{a}{3}\). Do đó \(\cos \widehat{CHK}=\frac{HK}{CH}=\frac{\frac{a}{3}}{\frac{a}{2}}=\frac{2}{3}.\) Chọn D. Câu hỏi 7 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a.\) Cạnh bên \(SA=x\) và vuông góc với mặt phẳng \(\left( ABCD \right).\) Xác định \(x\) để hai mặt phẳng \(\left( SBC \right)\) và \(\left( SCD \right)\) tạo với nhau một góc \({{60}^{0}}.\)
Đáp án: C Phương pháp giải: Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông Lời giải chi tiết:
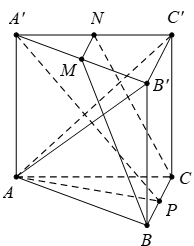
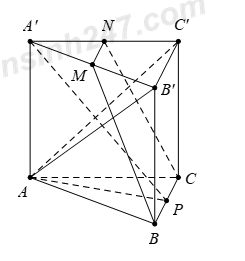
Từ A kẻ AH vuông góc với \(SB\,\,\,\,\left( H\in SB \right).\) Ta có \(\left\{ \begin{array}{l}SA \bot BC\\AB \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\) mà \(AH\bot SB\) suy ra \(AH\bot \left( SBC \right)\Rightarrow AH\bot SC\) Từ A kẻ AK vuông góc với \(SD\,\,\,\left( K\in SD \right),\) tương tự, chứng minh được \(SK\bot \left( SCD \right)\Rightarrow AK\bot SC\) Khi đó \(SC\bot \left( AHK \right)\) suy ra \(\widehat{\left( \left( SBC \right);\left( SCD \right) \right)}=\widehat{\left( AH;AK \right)}=\widehat{HAK}={{60}^{0}}.\) Lại có \(\Delta \,SAB=\Delta \,SAD\,\,\left( c.g.c \right)\Rightarrow AH=AK\) mà \(\widehat{HAK}={{60}^{0}}\) suy ra tam giác AHK đều. Tam giác SAB vuông tại A có \(\frac{1}{A{{H}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{B}^{2}}}=\frac{1}{{{x}^{2}}}+\frac{1}{{{a}^{2}}}\Rightarrow AH=\frac{xa}{\sqrt{{{x}^{2}}+{{a}^{2}}}}=AK=HK\) Suy ra \(SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{{{x}^{2}}-\frac{{{x}^{2}}{{a}^{2}}}{{{x}^{2}}+{{a}^{2}}}}=\frac{{{x}^{2}}}{\sqrt{{{x}^{2}}+{{a}^{2}}}}\Rightarrow \frac{SH}{SB}=\frac{{{x}^{2}}}{{{x}^{2}}+{{a}^{2}}}.\) Tương tự ta chứng minh được \(\frac{SK}{SC}=\frac{{{x}^{2}}}{{{x}^{2}}+{{a}^{2}}}\) \(\Rightarrow HK\)//\(BD\) suy ra \(\frac{SH}{SB}=\frac{HK}{BD}\Leftrightarrow \frac{{{x}^{2}}}{{{x}^{2}}+{{a}^{2}}}=\frac{xa}{\sqrt{{{x}^{2}}+{{a}^{2}}}.a\sqrt{2}}\Leftrightarrow \frac{x}{\sqrt{{{x}^{2}}+{{a}^{2}}}}=\frac{1}{\sqrt{2}}\Leftrightarrow 2{{x}^{2}}={{x}^{2}}+{{a}^{2}}\Rightarrow x=a.\) Chọn C. Câu hỏi 8 : Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có \(AB=2\sqrt{3}\) và \(A{A}'=2.\) Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của các cạnh \({A}'{B}',\,\,{A}'{C}'\) và \(BC.\) Côsin của góc tạo bởi hai mặt phẳng \(\left( A{B}'{C}' \right)\) và \(\left( MNP \right)\) bằng
Đáp án: B Phương pháp giải: Lời giải chi tiết: Dễ thấy \(\widehat{\left( A{B}'{C}' \right);\left( MNP \right)}=\widehat{\left( A{B}'{C}' \right);\left( MNCB \right)}\) \(\begin{align} & ={{180}^{0}}-\widehat{\left( A{B}'{C}' \right);\left( {A}'{B}'{C}' \right)}-\widehat{\left( MNBC \right);\left( {A}'{B}'{C}' \right)} \\ & ={{180}^{0}}-\widehat{\left( {A}'BC \right);\left( ABC \right)}-\widehat{\left( MNBC \right);\left( ABC \right)}. \\\end{align}\) Ta có \(\widehat{\left( {A}'BC \right);\left( ABC \right)}=\widehat{\left( {A}'P;AP \right)}=\widehat{{A}'PA}=\arctan \frac{2}{3}.\) Và \(\widehat{\left( MNBC \right);\left( ABC \right)}=\widehat{\left( SP;AP \right)}=\widehat{SPA}=\arctan \frac{4}{3},\) với \(S\) là điểm đối xứng với \(A\) qua \({A}',\) thì \(SA=2\,A{A}'=4.\) Suy ra \(\cos \widehat{\left( A{B}'{C}' \right);\left( MNP \right)}=\cos \left( {{180}^{0}}-\arctan \frac{2}{3}-\arctan \frac{4}{3} \right)=\frac{\sqrt{13}}{65}.\) Chọn B. Câu hỏi 9 : Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có \(AB=2\sqrt{3}\) và \(A{A}'=2.\) Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của các cạnh \({A}'{B}',\,\,{A}'{C}'\) và \(BC.\) Côsin của góc tạo bởi hai mặt phẳng \(\left( A{B}'{C}' \right)\) và \(\left( MNP \right)\) bằng
Đáp án: B Phương pháp giải: Sử dụng phương pháp xác định góc giữa hai mặt phẳng, tuy nhiên không sử dụng cách dựng hình truyền thống mà thông qua tính chất góc Lời giải chi tiết:
Dễ thấy \(\widehat{\left( \left( A{B}'{C}' \right);\left( MNP \right) \right)}=\widehat{\left( \left( A{B}'{C}' \right);\left( MNCB \right) \right)}\) \(\begin{array}{l} = {180^0} - \widehat {\left( {\left( {AB'C'} \right);\left( {A'B'C'} \right)} \right)} - \widehat {\left( {\left( {MNBC} \right);\left( {A'B'C'} \right)} \right)}\\ = {180^0} - \widehat {\left( {\left( {A'BC} \right);\left( {ABC} \right)} \right)} - \widehat {\left( {\left( {MNBC} \right);\left( {ABC} \right)} \right)}.\end{array}\) Ta có \(\widehat{\left( \left( {A}'BC \right);\left( ABC \right) \right)}=\widehat{\left( {A}'P;AP \right)}=\widehat{{A}'PA}=\arctan \frac{2}{3}.\) Và \(\widehat{\left( \left( MNBC \right);\left( ABC \right) \right)}=\widehat{\left( SP;AP \right)}=\widehat{SPA}=\arctan \frac{4}{3},\) với \(S\) là điểm đối xứng với \(A\) qua \({A}',\) thì \(SA=2\,A{A}'=4.\) Suy ra \(\cos \widehat{\left( A{B}'{C}' \right);\left( MNP \right)}=\left| \cos \left( {{180}^{0}}-\arctan \frac{2}{3}-\arctan \frac{4}{3} \right) \right|=\frac{\sqrt{13}}{65}.\) Chọn B. Câu hỏi 10 : Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh bằng \(a,\,\,\,\widehat{BAC}={{60}^{0}},\) cạnh \(SC\) vuông góc với đáy và \(SC=\frac{a\sqrt{6}}{2}.\) Tang của góc giữa hai mặt phẳng \(\left( SBD \right)\) và \(\left( SAD \right)\) bằng
Đáp án: C Phương pháp giải: Sử dụng phương pháp xác định góc giữa hai mặt phẳng trong không gian Lời giải chi tiết:
Gọi \(O\) là tâm của hình thoi \(ABCD,\) kẻ \(\left\{ \begin{align} CK\bot SO\,\,\,\left( K\in SO \right) \\ AH\bot SO\,\,\,\left( H\in SO \right) \\ \end{align} \right.\) Ta dễ dàng tính được BD = a, \(\text{AC=a}\sqrt{3}\) Xét tam giác vuông SCO có : \(CK=\frac{SC.CO}{\sqrt{S{{C}^{2}}+C{{O}^{2}}}}=\frac{\frac{a\sqrt{6}}{2}.\frac{a\sqrt{3}}{2}}{\sqrt{{{\left( \frac{a\sqrt{6}}{2} \right)}^{2}}+{{\left( \frac{a\sqrt{3}}{2} \right)}^{2}}}}=\frac{a}{\sqrt{2}}\) \(\begin{align} \Rightarrow AH=CK=\frac{a}{\sqrt{2}};\,\,SO=\sqrt{S{{C}^{2}}+O{{C}^{2}}}=\frac{3a}{2} \\ OK=\frac{C{{O}^{2}}}{SO}=\frac{\frac{3{{a}^{2}}}{4}}{\frac{3a}{2}}=\frac{a}{2} \\ \Rightarrow SH=SO+OH=SO+OK=\frac{3a}{2}+\frac{a}{2}=2a. \\ \end{align}\) Ta có : \(\left\{ \begin{align} BD\bot SC \\ BD\bot AC \\ \end{align} \right.\Rightarrow BD\bot \left( SAC \right)\Rightarrow BD\bot AH\) \(\left\{ \begin{align} AH\bot BD \\ AH\bot SO \\ \end{align} \right.\Rightarrow AH\bot \left( SBD \right)\Rightarrow AH\bot SD\) Kẻ \(HE\)\(\bot \)\(SD\) ta có : \(\left\{ \begin{align} SD\bot AH \\ SD\bot HE \\\end{align} \right.\Rightarrow SD\bot \left( AHE \right)\Rightarrow SD\bot AE\) \(\Rightarrow\widehat{\left( SBD \right);\left( SAD \right)}=\widehat{\left( HE;AE \right)}=\widehat{HEA}.\) Lại có \(SD=\sqrt{S{{C}^{2}}+C{{D}^{2}}}=\frac{a\sqrt{10}}{2}\Rightarrow HE.SD=DO.SH\Rightarrow HE=\frac{2a}{\sqrt{10}}.\) Do đó, giá trị \(\tan \widehat{HEA}=\frac{AH}{HE}=\frac{\sqrt{5}}{2}.\) Chọn C. Câu hỏi 11 : Cho hình lăng trụ đứng \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác cân, với \(AB=AC=a\) và góc \(\widehat{BAC}={{120}^{0}},\) cạnh bên \(A{A}'=a.\) Gọi \(I\) là trung điểm của \(C{C}'.\) Cosin của góc tạo bởi hai mặt phẳng \(\left( ABC \right)\) và \(\left( A{B}'I \right)\) bằng
Đáp án: C Phương pháp giải: Dựa vào phương pháp xác định góc giữa hai mặt phẳng và đưa vào tam giác vuông tính toán cosin góc giữa hai mặt phẳng Lời giải chi tiết: Vì \(A{A}'{B}'B\) là hình vuông cạnh \(a\)\(\Rightarrow \,\,A{{{B}'}^{2}}=2{{a}^{2}}.\) Ta có \(A{{I}^{2}}=A{{C}^{2}}+C{{I}^{2}}=\frac{5{{a}^{2}}}{4};\,\,{B}'{{I}^{2}}={B}'{{{C}'}^{2}}+{C}'{{I}^{2}}=B{{C}^{2}}+\frac{{{a}^{2}}}{4}\)Mà \(B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2.AB.AC.\cos {{120}^{0}}=3{{a}^{2}}\Rightarrow BC=a\sqrt{3}.\) Khi đó : \({B}'{{I}^{2}}=3{{a}^{2}}+\frac{{{a}^{2}}}{4}=\frac{13{{a}^{2}}}{4}\Rightarrow A{{{B}'}^{2}}+A{{I}^{2}}={B}'{{I}^{2}}\)\(\Rightarrow \,\,\Delta \,A{B}'I\) vuông tại \(A.\) Gọi \(D\) là giao điểm của \(BC\) và \({B}'I\,\,\Rightarrow \,\,AD=\left( ABC \right)\cap \left( A{B}'I \right).\) Kẻ \(CH\bot AD\) \(\left( H\in AD \right).\) Vì \(C\) là hình chiếu của \(I\) trên \(mp\,\,\left( ABC \right).\) Suy ra \(IH\bot AD\)\(\Rightarrow \,\,\widehat{IHC}\) chính là góc giữa hai mặt phẳng \(\left( ABC \right)\) và \(\left( A{B}'I \right).\) Trong tam giác \(B{B}'D\) có \(CI\) là đường trung bình \(\Rightarrow CD=CB=a\sqrt{3}.\) Xét tam giác \(ACD,\) có \(A{{D}^{2}}=A{{C}^{2}}+C{{D}^{2}}-2.AC.CD.\cos {{150}^{0}}=7{{a}^{2}}\Rightarrow AD=a\sqrt{7}.\) Lại có \(\frac{AC}{\sin \widehat{ADC}}=\frac{AD}{\sin {{150}^{0}}}\Rightarrow \sin \widehat{ADC}=\frac{1}{2\sqrt{7}}\Rightarrow CH=CD.\sin \widehat{ADC}=\frac{a\sqrt{21}}{14}.\) Tam giác \(IHC\) vuông \(\Rightarrow \,\,I{{H}^{2}}=C{{I}^{2}}+C{{H}^{2}}\Rightarrow \,\,IH=\frac{a\sqrt{70}}{14}.\) Vậy \(\cos \widehat{IHC}=\frac{CH}{IH}=\frac{\sqrt{30}}{10}.\) Chọn C.
Câu hỏi 12 : Cho hình lăng trụ ABC.A’B’C’ có mặt đáy ABC là tam giác đều cạnh AB = 2a. Hình chiếu vuông góc của A’ trên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng \({{60}^{0}}\). Tính tang của góc \(\varphi \) giữa hai mặt phẳng (ABC) và (BCC’B’).
Đáp án: A Phương pháp giải: Phương pháp xác định góc giữa 2 mặt phẳng (P) và (Q). Bước 1: Xác định \(d=\left( P \right)\cap \left( Q \right).\) Bước 2: Xác định \(a\subset \left( P \right);b\subset \left( Q \right)\) sao cho \(a\bot d;b\bot d\) Bước 3: Kết luận \(\widehat{\left( \left( P \right);\left( Q \right) \right)}=\widehat{\left( a;b \right)}\) Lời giải chi tiết: Gọi M, N lần lượt là trung điểm của BC và B’C’, E là trung điểm của BM, dễ thấy HE là đường trung bình của tam giác ABM nên HE // AM \(\Rightarrow HE//A'N\) \(\Rightarrow A';H;E;N\) đồng phẳng. Ta có: \(BC\bot AM\Rightarrow BC\bot HE;\,\,BC\bot A'H\Rightarrow BC\bot \left( A'HEN \right)\) \(\Rightarrow BC\bot NE\) \(\begin{array}{l} 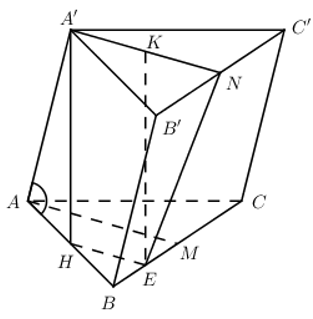
HE là đường trung bình của tam giác ABM\(\Rightarrow HE=\frac{1}{2}AM=\frac{1}{2}A'N\) Gọi K là trung điểm của A’N ta dễ dàng chứng minh được A’HEK là hình bình hành \(\begin{align} & \Rightarrow KE//A'H,\,\,KE=A'H \\ & \Rightarrow KE\bot \left( A'B'C' \right)\Rightarrow KE\bot KN \\ \end{align}\) \(\Rightarrow \Delta EKN\) vuông tại K \(\Rightarrow \tan \varphi =\tan \widehat{A'NE}=\frac{KE}{KN}=\frac{A'H}{\frac{1}{2}A'N}=\frac{2A'H}{A'N}\) Ta có \(\widehat{\left( A'A;\left( ABC \right) \right)}=\widehat{\left( A'A;HA \right)}=\widehat{A'AH}={{60}^{0}}\Rightarrow A'H=AH.\tan {{60}^{0}}=a\sqrt{3}.\) Tam giác A’B’C’ đều cạnh 2a \(\Rightarrow A'N=\frac{2a\sqrt{3}}{2}=a\sqrt{3}\) Vậy \(\tan \varphi =\frac{2A'H}{A'N}=\frac{2.a\sqrt{3}}{a\sqrt{3}}=2\) Chọn A.
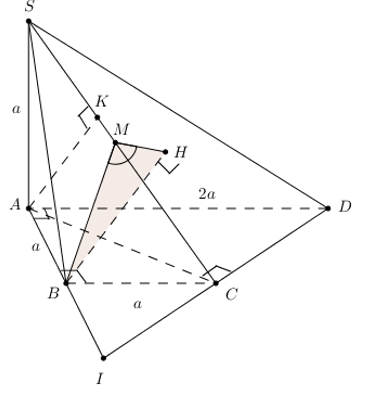
Câu hỏi 13 : Chóp S.ABCD, \(SA\bot \left( ABCD \right),\,\,SA=a\). ABCD là hình thang vuông ở A, D. \(AD=DC=\frac{AB}{2}=a\). Tính \(\widehat{\left( \left( SCD \right);\left( SBC \right) \right)}\).
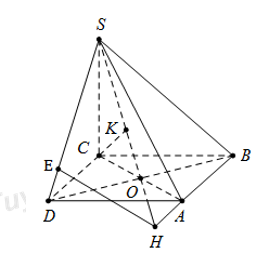
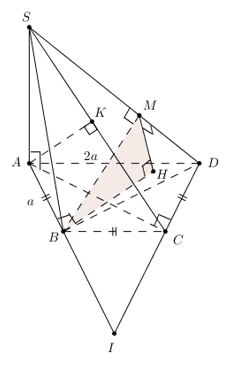
Đáp án: A Phương pháp giải: Lời giải chi tiết: * Vẽ \(DH\bot \left( SBC \right)\). Vẽ \(HM\bot SC\Rightarrow \widehat{\left( \left( SCD \right);\left( SBC \right) \right)}=\widehat{M}\). * Nối \(AD\cap BC=I\). Ta có : \(DH=d\left( D;\left( SBC \right) \right)=\frac{1}{2}d\left( A;\left( SBC \right) \right)=\frac{1}{2}AK\) \(\begin{align}+\,\,\frac{1}{A{{K}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{C}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{2{{a}^{2}}} \\ \Rightarrow AC=\frac{a\sqrt{6}}{3}\Rightarrow DH=\frac{a\sqrt{6}}{6} \\ \end{align}\). + Tam giác vuông SCD : \(\begin{align}\frac{1}{D{{M}^{2}}}=\frac{1}{S{{D}^{2}}}+\frac{1}{C{{D}^{2}}}=\frac{1}{2{{a}^{2}}}+\frac{1}{{{a}^{2}}}=\frac{3}{2{{a}^{2}}}\Rightarrow DM=\frac{a\sqrt{6}}{3} \\ \Rightarrow \sin\widehat{M}=\frac{DH}{DM}=\frac{\frac{a\sqrt{6}}{6}}{\frac{a\sqrt{6}}{3}}=\frac{1}{2}\Rightarrow \widehat{M}={{30}^{0}} \\ \end{align}\) Chọn đáp án A. Câu hỏi 14 : Chóp \(S.ABCD,\,\,SA\bot \left( ABCD \right),\,\,SA=a,\,\,ABCD\) là \(\frac{1}{2}\) lục giác đều có \(AB=BC=CD=a\). Tính \(\widehat{\left( \left( SBD \right);\left( SCD \right) \right)}\).
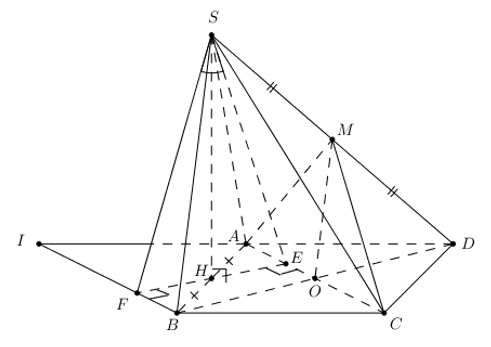
Đáp án: C Phương pháp giải: Lời giải chi tiết: * Lưu ý : \(\widehat{ABD}=\widehat{ACD}={{90}^{0}}\) \(\left\{ \begin{align} BD\bot AB \\ BD\bot SA \\ \end{align} \right.\Rightarrow BD\bot SB\) * Chọn B. Vẽ giả tưởng \(BH\bot \left( SCD \right)\). Vẽ \(HM\bot \) giao tuyến SD \(\Rightarrow \widehat{\left( \left( SBD \right);\left( SCD \right) \right)}=\widehat{HMB}=\widehat{{{M}_{1}}}\). * Tam giác vuông SBD : \(\frac{1}{B{{M}^{2}}}=\frac{1}{2{{a}^{2}}}+\frac{1}{3{{a}^{2}}}=\frac{5}{6{{a}^{2}}}\Rightarrow BM=\frac{a\sqrt{6}}{\sqrt{5}}\). * \(BH=d\left( B;\left( SCD \right) \right)=\frac{1}{2}d\left( A;\left( SCD \right) \right)=\frac{1}{2}AK\) Tam giác vuông SAC : \(\frac{1}{A{{K}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{3{{a}^{2}}}=\frac{4}{3{{a}^{2}}}\Rightarrow AK=\frac{a\sqrt{3}}{2}\Rightarrow BH=\frac{a\sqrt{3}}{4}\). * Tam giác BHM : \(\sin \widehat{{{M}_{1}}}=\frac{BH}{BM}=\frac{a\sqrt{3}}{4}:\frac{a\sqrt{6}}{\sqrt{5}}=\frac{\sqrt{10}}{8}\). Chọn đáp án C. Câu hỏi 15 : Chóp S.ABCD, \(\left( SAB \right)\bot \left( ABCD \right),\,\,\Delta SAB\) đều, \(ABCD\) là hình vuông, \(AB=a\). M là trung điểm của SD. Tính \(\widehat{\left( \left( MAC \right);\left( SAC \right) \right)}\).
Đáp án: A Phương pháp giải: Lời giải chi tiết: * Phương pháp thay thế góc * Qua B vẽ d // AC, \(d\cap AD=I\). Nối \(AC\cap BD=O,\,\,\Delta SBD\) có OM là đường trung bình \(\Rightarrow \left\{ \begin{align} OM//SB \\ BI//AC \\ \end{align} \right.\) \(\Rightarrow \left( MAC \right)//\left( SBI \right)\Rightarrow \widehat{\left( \left( MAC \right);\left( SAC \right) \right)}=\widehat{\left( \left( SBI \right);\left( SAC \right) \right)}\) * Vẽ \(SH\bot AB\Rightarrow SH\bot \left( ABCD \right).\) Vẽ \(HE\bot AC;\,\,HF\bot IB\Rightarrow \left\{ \begin{align} SE\bot AC \\ SF\bot IB \\ \end{align} \right.\). \(\Rightarrow \widehat{\left( \left( SBI \right);\left( SAC \right) \right)}=\widehat{ESF}\) (cá biệt 2). * \(HE=BO=\frac{a}{\sqrt{2}},\,\,HE=\frac{a}{2\sqrt{2}}\) * Tam giác vuông SHE : \(SE=\sqrt{\frac{3{{a}^{2}}}{4}+\frac{{{a}^{2}}}{8}}=\frac{a\sqrt{7}}{\sqrt{8}}=\frac{a\sqrt{7}}{2\sqrt{2}}\) * \(\cos \widehat{ESF}=\frac{E{{F}^{2}}-S{{E}^{2}}-S{{F}^{2}}}{-2SE.SF}=\frac{\frac{{{a}^{2}}}{2}-\frac{7{{a}^{2}}}{8}-\frac{7{{a}^{2}}}{8}}{-2.\frac{7{{a}^{2}}}{8}}=\frac{5}{7}\) Chọn đáp án A. Câu hỏi 16 : Cho hình lăng trụ \(ABC.{A}'{B}'{C}'\) có \({A}'.ABC\) là tứ diện đều cạnh \(a\). Gọi \(M,\,N\) lần lượt là trung điểm của \(A{A}'\) và \(B{B}'\). Tính \(\tan \) của góc hợp bởi hai mặt phẳng \(\left( ABC \right)\) và \(\left( CMN \right)\).
Đáp án: C Phương pháp giải: Dựng hình, sử dụng phương pháp xác định góc giữa hai mặt phẳng hoặc áp dụng phương pháp tọa độ hóa (hình giải tích Oxyz) để tính góc Lời giải chi tiết: Ta có \(\left\{ \begin{align} & \left( ABC \right)\cap \left( CMN \right)=\left\{ C \right\} \\ & AB//MN \\ \end{align} \right.\) \(\Rightarrow \left( ABC \right)\cap \left( CMN \right)=\Delta \) (\(\Delta \) là đường thẳng đi qua \(C\) và // với \(AB\)). Gọi \(E,\,\,I\) lần lượt là trung điểm của \(AB\) và \(MN\). Gọi \(F\) là trung điểm của \(MI\). Suy ra \(\left\{ \begin{align} & EC\bot AB \\ & FC\bot MN \\ \end{align} \right.\)\(\Rightarrow \left( \widehat{\left( ABC \right),\,\left( MNC \right)} \right)=\widehat{ECF}\) Ta có \(MF=\frac{1}{4}MN=\frac{a}{4},\) \(MC=\sqrt{A{{C}^{2}}-A{{M}^{2}}}=\frac{a\sqrt{3}}{2}\) \(\Rightarrow CF=\sqrt{M{{C}^{2}}-M{{F}^{2}}}=\frac{a\sqrt{11}}{4}\) Xét \(\Delta EBC\) vuông tại \(E,\) có \(EC=\sqrt{B{{C}^{2}}-B{{E}^{2}}}=\sqrt{{{a}^{2}}-{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{3}}{2}\) và \(EF=\frac{1}{2}E{A}'=\frac{a\sqrt{3}}{4}\). Áp dụng định lý \(\operatorname{cosin}\) cho tam giác \(ECF,\) \(\cos \widehat{ECF}=\frac{E{{C}^{2}}+F{{C}^{2}}-E{{F}^{2}}}{2EC.FC}=\frac{5\sqrt{33}}{33}\) Vậy \(\tan \widehat{ECF}=\sqrt{\frac{1}{{{\cos }^{2}}\widehat{ECF}}-1}=\frac{2\sqrt{2}}{5}\). Chọn C Câu hỏi 17 : Cho hình vuông ABCD cạnh a. Trên hai tia Bx, Dy vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và cùng chiều lấy lần lượt hai điểm M, N sao cho \(BM = \frac{a}{2},DN = a.\). Tính góc \(\varphi \) giữa hai mặt phẳng \(\left( {AMN} \right)\,và \,\left( {CMN} \right).\)
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 18 : Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật \(ABCD\) biết \(AB=2\), \(AD=3\), \(SD=\sqrt{14}\) Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi \(M\) là trung điểm của \(SC\) Côsin của góc tạo bởi hai mặt phẳng \((SBD)\) và \((MBD)\) bằng
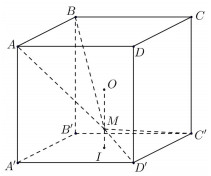
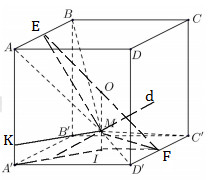
Đáp án: B Phương pháp giải: Lời giải chi tiết: Câu hỏi 19 : Cho hình lập phương ABCD.A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho MO = 2MI (tham khảo hình vẽ). Khi đó sin của góc tạo bởi hai mặt phẳng (MC’D’) và (MAB) bằng
Đáp án: D Phương pháp giải: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và vuông góc với giao tuyến. Lời giải chi tiết:
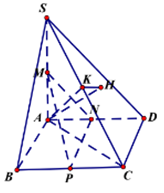
Ta có AB // C’D’ \( \Rightarrow \) Giao tuyến của hai mặt phẳng (MAB) và (MC’D’) là đường thẳng đi qua M và song song với AB, C’D’. Gọi d là đường giao tuyến của hai mặt phẳng trên. Do \(M \in OI \Rightarrow MA = MB \Rightarrow \Delta MAB\) cân tại M, tương tự \(\Delta MC'D'\) cân tại M. Gọi E, F lần lượt là trung điểm của AB và C’D’ ta có: \(\left\{ \begin{array}{l}ME \bot AB \Rightarrow ME \bot d\\MF \bot C'D' \Rightarrow MF \bot d\end{array} \right. \Rightarrow \widehat {\left( {\left( {MAB} \right);\left( {MC'D'} \right)} \right)} = \widehat {\left( {ME;MF} \right)}\) Kẻ MK // A’I, ta có \(A'K = MI = \frac{1}{3}OI = \dfrac{1}{6}AA'\) Gọi cạnh hình lập phương là 1 \( \Rightarrow A'K = \dfrac{1}{6} \Rightarrow AK = \dfrac{5}{6}\) Do A’B’C’D’ là hình vuông cạnh 1 \( \Rightarrow KM = A'I = \dfrac{1}{{\sqrt 2 }} \Rightarrow AM = \sqrt {A{K^2} + K{M^2}} = \sqrt {\frac{{43}}{{36}}} \) Xét tam giác vuông AME có \(ME = \sqrt {A{M^2} - A{E^2}} = \sqrt {\dfrac{{43}}{{36}} - \dfrac{1}{4}} = \dfrac{{\sqrt {34} }}{6}\) Ta có \(IF = \dfrac{1}{2} \Rightarrow MF = \sqrt {M{I^2} + I{F^2}} = \sqrt {{{\left( {\dfrac{1}{6}} \right)}^2} + {{\left( {\dfrac{1}{2}} \right)}^2}} = \dfrac{{\sqrt {10} }}{6}\) \(EF = AD' = \sqrt 2 \) Áp dụng định lí Cosin trong tam giác EFM có: \(\cos \widehat {EMF} = \dfrac{{M{E^2} + M{F^2} - E{F^2}}}{{2ME.MF}} = \dfrac{{\dfrac{{34}}{{36}} + \dfrac{{10}}{{36}} - 2}}{{2\dfrac{{\sqrt {34} }}{6}.\dfrac{{\sqrt {10} }}{6}}} = - \dfrac{{7\sqrt {85} }}{{85}}\) \(\begin{array}{l} \Rightarrow \cos \widehat {\left( {ME;MF} \right)} = \dfrac{{7\sqrt {85} }}{{85}} = \cos \widehat {\left( {\left( {MAB} \right);\left( {MC'D'} \right)} \right)}\\ \Rightarrow \sin \widehat {\left( {\left( {MAB} \right);\left( {MC'D'} \right)} \right)} = \sqrt {1 - {{\left( {\dfrac{{7\sqrt {85} }}{{85}}} \right)}^2}} = \dfrac{{6\sqrt {85} }}{{85}}\end{array}\) Chọn D. Câu hỏi 20 : Cho khốic chóp \(SABCD\) có đáy là hình bình hành, \(AB = 3,\;AD = 4,\;\angle BAD = {120^0}.\) Cạnh bên \(SA = 2\sqrt 3 \) vuông góc với đáy. Gọi \(M,\;N,\;P\) lần lượt là trung điểm các cạnh \(SA,\;AD\) và \(BC,\;\;\alpha \) là góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {MNP} \right).\) Chọn khẳng định đúng trong các khẳng định sau đây.
Đáp án: A Phương pháp giải: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng thuộc hai mặt phẳng cùng vuông góc với giao tuyến chung của hai mặt phẳng đó. Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}MN//SD\\NP//CD\end{array} \right. \Rightarrow \left( {MNP} \right)//\left( {SCD} \right)\) \( \Rightarrow \angle \left( {\left( {SAC} \right),\;\left( {MNP} \right)} \right) = \angle \left( {\left( {SAC} \right),\;\left( {SCD} \right)} \right) = \alpha .\) Gọi H là hình chiếu vuông góc của A xuống (SCD), K là hình chiếu của H xuống SC \( \Rightarrow \alpha = \angle AKH.\) Ta có: \({V_{SACD}} = \frac{1}{2}{V_{SABCD}} = \frac{1}{3}.SA.{S_{ABCD}} = \frac{1}{3}SA.2{S_{ABD}} = \frac{1}{3}.SA.AB.AD.\sin \angle BAD = \frac{1}{3}.\frac{1}{2}.3.4.\sqrt 3 .2\sqrt 3 = 6.\) Có: \(A{C^2} = 13 \Rightarrow S{C^2} = S{A^2} + A{C^2} = 25.\) \(\begin{array}{l}SD = \sqrt {S{A^2} + A{D^2}} = \sqrt {12 + 16} = \sqrt {28} \\ \Rightarrow {S_{SCD}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \sqrt {54} = 3\sqrt 6 .\\ \Rightarrow AH = d\left( {A;\;\left( {CSD} \right)} \right) = \frac{{3{V_{SACD}}}}{{{S_{SCD}}}} = \frac{{3.6}}{{3\sqrt 6 }} = \sqrt 6 .\\AK = \frac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{2\sqrt {39} }}{5}.\\ \Rightarrow \sin \alpha = \frac{{AH}}{{AK}} = \sqrt 6 .\frac{5}{{2\sqrt {39} }} = \frac{{5\sqrt {26} }}{{26}} \Rightarrow \alpha \in \left( {{{60}^0};\;{{90}^0}} \right).\end{array}\) Chọn A. Quảng cáo
|