Câu hỏi:
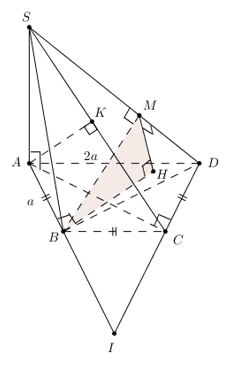
Chóp \(S.ABCD,\,\,SA\bot \left( ABCD \right),\,\,SA=a,\,\,ABCD\) là \(\frac{1}{2}\) lục giác đều có \(AB=BC=CD=a\). Tính \(\widehat{\left( \left( SBD \right);\left( SCD \right) \right)}\).
- A \(\arcsin \frac{1}{8}\)
- B \(\arcsin \frac{\sqrt{2}}{8}\)
- C \(\arcsin \frac{\sqrt{10}}{8}\)
- D \(\arcsin \frac{5}{8}\)
Phương pháp giải:
Lời giải chi tiết:
* Lưu ý : \(\widehat{ABD}=\widehat{ACD}={{90}^{0}}\)
\(\left\{ \begin{align} BD\bot AB \\ BD\bot SA \\ \end{align} \right.\Rightarrow BD\bot SB\)
* Chọn B. Vẽ giả tưởng \(BH\bot \left( SCD \right)\).
Vẽ \(HM\bot \) giao tuyến SD \(\Rightarrow \widehat{\left( \left( SBD \right);\left( SCD \right) \right)}=\widehat{HMB}=\widehat{{{M}_{1}}}\).
* Tam giác vuông SBD : \(\frac{1}{B{{M}^{2}}}=\frac{1}{2{{a}^{2}}}+\frac{1}{3{{a}^{2}}}=\frac{5}{6{{a}^{2}}}\Rightarrow BM=\frac{a\sqrt{6}}{\sqrt{5}}\).
* \(BH=d\left( B;\left( SCD \right) \right)=\frac{1}{2}d\left( A;\left( SCD \right) \right)=\frac{1}{2}AK\)
Tam giác vuông SAC : \(\frac{1}{A{{K}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{3{{a}^{2}}}=\frac{4}{3{{a}^{2}}}\Rightarrow AK=\frac{a\sqrt{3}}{2}\Rightarrow BH=\frac{a\sqrt{3}}{4}\).
* Tam giác BHM : \(\sin \widehat{{{M}_{1}}}=\frac{BH}{BM}=\frac{a\sqrt{3}}{4}:\frac{a\sqrt{6}}{\sqrt{5}}=\frac{\sqrt{10}}{8}\).
Chọn đáp án C.