Phương pháp giải:

Đặt \(\ln x = t\). Đưa về tích phân biến t.

Lời giải chi tiết:

Đặt \(\ln x = t\)

=> \(dt = \dfrac{{dx}}{x}\)

Đổi cận:

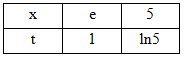
\(\begin{array}{l} \Rightarrow {\rm{I}} = \int_e^5 {\dfrac{{\ln {\rm{x}} + 3}}{{\rm{x}}}} {\rm{dx = }}\int\limits_1^{\ln 5} {\left( {t + 3} \right)dt} \\ = \dfrac{{{{\ln }^2}5}}{2} + 3\ln 5 - \dfrac{7}{2}\\ \Rightarrow a = 3,b = 7\end{array}\)