Phương pháp giải:

- Đưa hàm số về dạng phương trình bậc nhất ẩn $m$: $Am + B = 0$, tìm điều kiện để phương trình nghiệm đúng $A = B = 0$, từ đó xác định điểm cố định $M$ mà đường thẳng $d$ đi qua.

- Sử dụng định lí đường vuông góc và đường xiên, chứng minh $d\left( {O;d} \right) \le OM$. Dấu “=” xảy ra $\Leftrightarrow OM \bot d$.

Lời giải chi tiết:

Ta có:

$\begin{array}{l}\,\,\,\,\,y = \left( {m - 1} \right)x + 4m\\ \Leftrightarrow mx - x + 4m - y = 0\\ \Leftrightarrow \left( {x - 4} \right)m - x - y = 0\end{array}$

Phương trình trên đúng với mọi $m$ khi và chỉ khi $\left\{ \begin{array}{l}x - 4 = 0\\ - x - y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y =  - 4\end{array} \right.$.

$\Rightarrow$ Đường thẳng $\left( d \right)$ đi qua điểm $M\left( {4; - 4} \right)\,\,\forall m$.

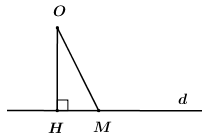
Gọi $H$ là hình chiếu vuông góc của $O$ lên đường thẳng $d$, ta có $d\left( {O;d} \right) = OH \le OM$ (quan hệ vuông góc giữa đường kính và dây cung).

Do đó khoảng cách từ $O$ đến đường thẳng $d$ đạt GTLN khi và chỉ khi

$d\left( {O;d} \right) = OM = \sqrt {{{\left( {4 - 0} \right)}^2} + {{\left( { - 4 - 0} \right)}^2}}  = 4\sqrt 2$.

Chọn C.