Câu hỏi:
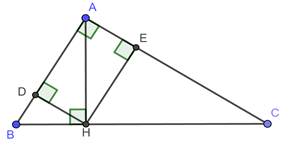
Cho tam giác \(ABC\) vuông tại \(A\,\,\,\left( {AB < AC} \right)\) với đường cao \(AH\). Goi \(D\) và \(E\) lần lượt là hình chiếu của \(H\) trên \(AB\) và \(AC\). Chứng minh:
a) \(AB.AD = AC.AE\) b) \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH}}{{CH}}\)
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông và tính chất bắc cầu.
Lời giải chi tiết:
a) \(AB.AD = AC.AE\)
Áp dụng hệ thức lượng trong \(\Delta ABH\) vuông tại \(H\) có đường cao \(DH\) ta có: \(AB.AD = A{H^2}\,\,\,\,\left( 1 \right)\)
Áp dụng hệ thức lượng trong \(\Delta ACH\) vuông tại \(H\) có đường cao \(HE\) ta có: \(AE.AC = A{H^2}\left( 2 \right)\)
Từ \(\left( 1 \right),\,\,\,\left( 2 \right) \Rightarrow \)\(AB.AD = AC.AE\,\,\,\left( { = A{H^2}} \right).\)
b) \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH}}{{CH}}\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(\left\{ \begin{array}{l}BH.BC = A{B^2}\\CH.BC = A{C^2}\end{array} \right..\)
Ta có: \(\left. \begin{array}{l}A{B^2}.CH = BH.BC.CH\\A{C^2}.BH = CH.BC.BH\end{array} \right\} \Rightarrow A{B^2}.CH = A{C^2}.BH\)\( \Rightarrow \frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH}}{{CH}}\,\,\,\left( {dpcm} \right)\)