Câu hỏi:
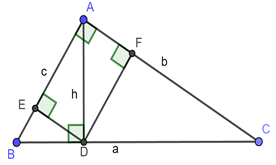
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AD.\) Đặt \(BC = a,AB = c,AC = b,AD = h\).
a) Chứng minh rằng số đo độ dài \(h;b + c;a + h\) là độ dài ba cạnh của một tam giác vuông
b) Gọi \(E;F\) lần lượt là hình chiếu của \(D\) lên \(AB;\,\,AC.\) Chứng minh \(EA.EB + FE.FB = DB.DC\)
c) Chứng minh hệ thức trên đúng với mọi vị trí của \(D\) bất kì trên cạnh \(BC.\)
Phương pháp giải:
a) Sử dụng định lý Pitago và hệ thức lượng trong tam giác vuông để chứng minh.
b) Sử dụng hệ thức lượng trong tam giác vuông để chứng minh.
Lời giải chi tiết:
a) Chứng minh rằng số đo độ dài \(h;b + c;a + h\) là độ dài ba cạnh của một tam giác vuông.
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow {b^2} + {c^2} = {a^2}\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AD\) ta có:
\( \Rightarrow AD.BC = AB.AC\)\( \Leftrightarrow bc = ah\)
Ta có: \({h^2} + {\left( {b + c} \right)^2} = {h^2} + {b^2} + 2bc + {c^2}\)
Mà \({b^2} + {c^2} = {a^2};bc = ah\left( {cmt} \right)\)
\( \Rightarrow {h^2} + {\left( {b + c} \right)^2} = {h^2} + {a^2} + 2ah = {\left( {a + h} \right)^2}\)
Vậy số đo độ dài \(h;b + c;a + h\) là độ dài ba cạnh của một tam giác vuông (Định lý Pitago đảo).
b. Gọi \(E;F\) lần lượt là hình chiếu của \(D\) lên \(AB;AC\) . Chứng minh \(EA.EB + FA.FC = DB.DC\)
Áp dụng hệ thức lượng trong \(\Delta ABD\) vuông tại \(D\) có đường cao \(ED\) ta có: \(EA.EB = E{D^2}\)
Áp dụng hệ thức lượng trong \(\Delta ACD\) vuông tại \(D\) có đường cao \(DF\) ta có: \(FA.FC = F{D^2}\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AD\) ta có: \(DB.DC = A{D^2}\)
Xét tứ giác \(AFDE\)có \(\angle A = \angle F = \angle E = {90^0}\)
\( \Rightarrow AFDE\) là hình chữ nhật \( \Rightarrow \angle D = {90^0}\) và \(AD = EF\) (tính chất hình chữ nhật)
Áp dụng định lý Pitago cho \(\Delta EDF\) vuông tại \(D\) có: \(D{E^2} + D{F^2} = E{F^2}\)
Mà \(EA.EB = D{E^2}\); \(FA.FC = D{F^2}\)
\( \Rightarrow EA.EB + FA.FC = E{F^2}\)
Mà \(AD = EF\)\( \Rightarrow EA.EB + FA.FC = A{D^2}\)
Mặt khác \(DB.DC = A{D^2}\)
\( \Rightarrow EA.EB + FA.FC = DB.DC\,\,\,\left( {\,dpcm} \right)\)
c) Chứng minh hệ thức trên đúng với mọi vị trí của \(D\) bất kì trên cạnh \(BC\)
Với mọi vị trí của \(D\) bất kì trên cạnh \(BC\)thì tứ giác\(AFDE\) luôn là hình chữ nhật \( \Rightarrow \hat D = {90^0}\)và \(AD = EF\)
Vì vậy hệ thức trên luôn đúng.