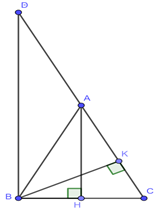
Câu hỏi:
Cho \(\Delta ABC\) cân tại \(A\) có đường cao là \(AH\) và \(BK\). Kẻ đường thẳng vuông góc với \(BC\) tại \(B\) cắt tia \(CA\) tại \(D\).
a) Chứng minh \(BD = 2AH\)
b) Chứng minh \(\frac{1}{{B{K^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{4A{H^2}}}\)
Phương pháp giải:
a) Sử dụng tính chất đường trung bình của tam giác.
b) Sử dụng hệ thức lượng trong tam giác vuông để chứng minh đẳng thức.
Lời giải chi tiết:
a) Chứng minh \(BD = 2AH\)
Ta có: \(\Delta ABC\) cân tại \(A \Rightarrow AH\) là đường cao đồng thời là đường trung tuyến (định lý)
\( \Rightarrow H\)trung điểm \(BC\)
Ta có: \(\left. \begin{array}{l}AH \bot BC\,\,\,\left( {gt} \right)\\BD \bot BC\,\,\left( {gt} \right)\end{array} \right\} \Rightarrow AH//BD\)
Xét \(\Delta CBD\) có:
\(H\) trung điểm \(BC\)(cmt)
\(AH//BD\)(cmt)
là đường trung bình của \(\Delta ABD\)(định lý đảo)
\( \Rightarrow AH = \frac{1}{2}BD\left( {tc} \right) \Leftrightarrow BD = 2AH\) (đpcm)
b) Chứng minh \(\frac{1}{{B{K^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{4A{H^2}}}\)
Xét \(\Delta CBD\) vuông tại \(B\) có:
\(BK\) là đường cao ứng với cạnh huyền \(DC\)
\( \Rightarrow \frac{1}{{B{K^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{B{D^2}}}\)(hệ thức lượng trong tam giác vuông)
Mà \(BD = 2AH\)
\( \Rightarrow \frac{1}{{B{K^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{4A{H^2}}}\)(đpcm)