Câu hỏi:
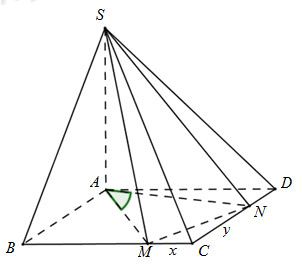
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Hai điểm M, N lần lượt thay đổi trên cạnh CB và CD, đặt CM = x, CN = y. Tìm hệ thức liên hệ giữa x và y để hai mặt phẳng (SAM) và (SAN) tạo với nhau một góc \({90^0}\)?
- A \(x + y = 2a\)
- B \(x - y = 2a\)
- C \(x + y = a\)
- D \(x - y = a\)
Phương pháp giải:
+) Xác định góc giữa (SAM) và (SAN) bằng cách xác định hai đường thẳng lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến SA.
+) Sử dụng định lí Pytago tính các đoạn thẳng AM, AN, MN theo a, x, y.
+) Áp dụng định lí Pytago đảo chứng minh tam giác AMN vuông.
Lời giải chi tiết:
\(\begin{array}{l}\left. \begin{array}{l}\left( {SAM} \right) \cap \left( {SAN} \right) = SA\\AM \bot SA\\AN \bot SA\end{array} \right\}\\ \Rightarrow \widehat {\left( {\left( {SAM} \right);\left( {SAN} \right)} \right)} = \widehat {\left( {AM;AN} \right)} = \widehat {MAN} = {90^0}\end{array}\)
Ta có:
\(\begin{array}{l}A{M^2} = A{B^2} + B{M^2} = {a^2} + {\left( {a - x} \right)^2}\\A{N^2} = A{D^2} + D{N^2} = {a^2} + {\left( {a - y} \right)^2}\\M{N^2} = {x^2} + {y^2}\end{array}\)
Xét tam giác vuông AMN có:
\(\begin{array}{l}M{N^2} = A{M^2} + A{N^2}\\ \Rightarrow {x^2} + {y^2} = {a^2} + {\left( {a - x} \right)^2} + {a^2} + {\left( {a - y} \right)^2}\\ \Leftrightarrow 0 = 4{a^2} - 2ax - 2ay\\ \Leftrightarrow x + y = 2a\end{array}\)
Chọn A.


















