Phương pháp giải:

+) Gọi H là tâm của tam giác đều ABC\( \Rightarrow A'H \bot \left( {ABC} \right)\)

+) Gọi E là trung điểm của AB, chứng minh \(\widehat {\left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {HE;A'E} \right)}\).

Lời giải chi tiết:

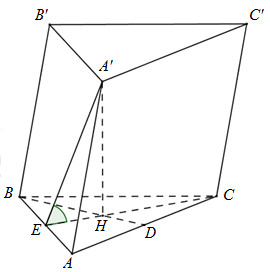
Vì \(A'A = A'B = A'C = a\sqrt {\frac{7}{{12}}} ,\Delta ABC\)đều nên chóp\(A'.ABC\)là chóp đều.

Gọi H là tâm của tam giác đều ABC\( \Rightarrow A'H \bot \left( {ABC} \right)\)

Gọi E là trung điểm của AB thì \(HE \bot AB\)

Lại có: \(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot AB\)

\( \Rightarrow AB \bot \left( {A'HE} \right) \Rightarrow AB \bot A'E\)

Ta có:

\(\begin{array}{l}\left. \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {ABC} \right) = AB\\HE \bot AB\\AE \bot AB\end{array} \right\}\\ \Rightarrow \widehat {\left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {HE;A'E} \right)} = \widehat {A'EH}\end{array}\)

(Vì \(\Delta A'HE\) vuông tại H \( \Rightarrow \widehat {A'EH} < {90^0}\))

Ta có: \(CE = \dfrac{{a\sqrt 3 }}{2} \Rightarrow HE = \dfrac{1}{3}CE = \dfrac{{a\sqrt 3 }}{6};HC = \dfrac{2}{3}CE = \dfrac{{a\sqrt 3 }}{3}\)

\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot CH\)

Xét tam giác vuông\(A'HC\)có: \(A'H = \sqrt {A'{C^2} - H{C^2}}  = \sqrt {\dfrac{7}{{12}}{a^2} - \dfrac{1}{3}{a^2}}  = \dfrac{a}{2}\)

Xét tam giác vuông \(A'HE\) có: \(\tan \widehat {A'EH} = \dfrac{{A'H}}{{EH}} = \dfrac{{\dfrac{a}{2}}}{{\dfrac{{a\sqrt 3 }}{6}}} = \sqrt 3  \Rightarrow \widehat {A'EH} = {60^0}\)

Chọn D.