Phương pháp giải:

+) Xác định góc giữa cạnh bên và mặt đáy.

+) Gọi E là trung điểm của AB, chứng minh \(\widehat {\left( {\left( {SAB} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SE;OE} \right)}\)

Lời giải chi tiết:

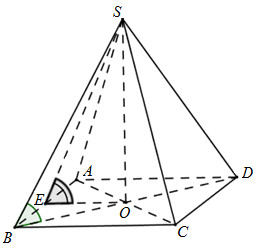
Gọi O là tâm hình vuông ABCD. Vì chóp S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\)

Ta có OB là hình chiếu của SB lên (ABCD) nên

\(\widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {\left( {SB;OB} \right)} = \widehat {SBO} = \varphi \,\,\left( {\widehat {SBO} < {{90}^0}} \right)\)

Gọi E là trung điểm của AB

Tam giác SAB cân tại S nên \(SE \bot AB\)

\(\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SE \bot AB\\OE \bot AB\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SE;OE} \right)} = \widehat {SEO}\) (Vì \(\widehat {SEO} < {90^0}\) )

Ta có: \(OB = \frac{{a\sqrt 2 }}{2};OE = \dfrac{a}{2}\)

Xét tam giác vuông SOB có: \(\tan \varphi  = \dfrac{{SO}}{{OB}} \Rightarrow SO = \dfrac{{a\sqrt 2 }}{2}\tan \varphi \)

Xét tam giác vuông SOE có: \(\tan \widehat {SEO} = \dfrac{{SO}}{{OE}} \Rightarrow SO = \dfrac{a}{2}.\tan \widehat {SEO}\)

\( \Rightarrow \dfrac{{a\sqrt 2 }}{2}\tan \varphi  = \frac{a}{2}\tan \widehat {SEO} \Rightarrow \tan \widehat {SEO} = \sqrt 2 \tan \varphi \)

Chọn B.