Bài 9 trang 93 SGK Hình học 10Tìm tọa độ các đỉnh, các tiêu điểm và vẽ elip đó. Quảng cáo
Đề bài Cho elip \((E) = {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) . Tìm tọa độ các đỉnh, các tiêu điểm và vẽ elip đó. Video hướng dẫn giải Lời giải chi tiết
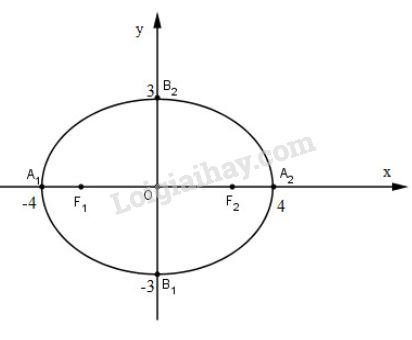
Phương trình chính tắc của Elip \((E) = {{{x^2}} \over {16}} + {{{y^2}} \over 9} = 1\) có dạng là: \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\) Ta có: \(\eqalign{ +) Tọa độ các đỉnh \(A_1(-4;0), A_2(4; 0), B_1(0; -3)\) và \(B_2(0; 3)\) +) Tọa độ các tiêu điểm \(F_1(-\sqrt7; 0)\) và \(F_2(\sqrt7; 0)\) Loigiaihay.com
|




















Danh sách bình luận