Bài 9 trang 50 SGK Đại số 10Xét chiều biến thiên và vẽ đồ thị của các hàm số Quảng cáo
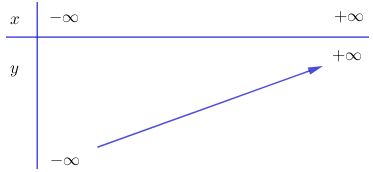
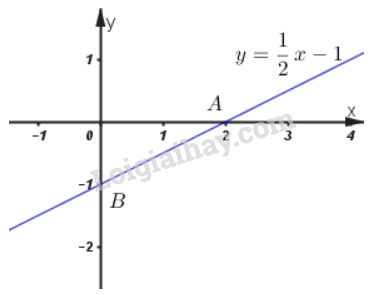
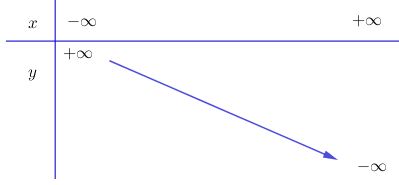
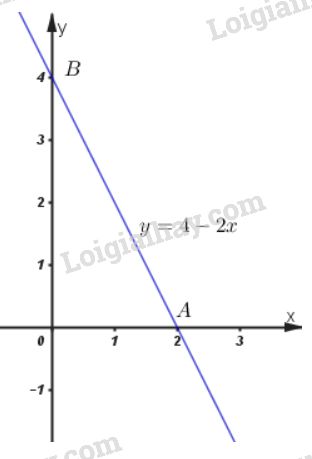
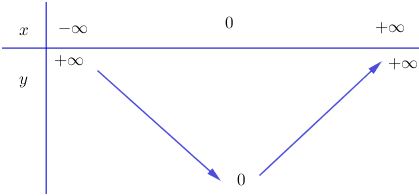
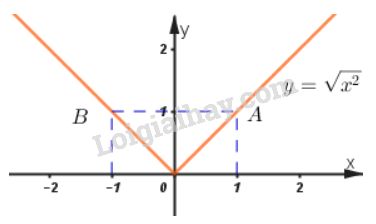
Video hướng dẫn giải Xét chiều biến thiên và vẽ đồ thị của các hàm số LG a \(y = {1 \over 2}x - 1\) Phương pháp giải: +) Hàm số \(y=a x + b\) đồng biến trên \(R\) khi \(a >0\) và nghịch biến trên \(R\) khi \(a<0.\) Lời giải chi tiết: \(y = {1 \over 2}x - 1\) Ta có: \(a = \frac{1}{2} > 0\) nên hàm số đồng biến trên R. Bảng biến thiên Đồ thị hàm số: + Cho x=0 thì \(y = \frac{1}{2}.0 - 1 = - 1\) nên đồ thị giao với trục tung tại \(B(0; \,-1)\) + Cho y=0 thì \(0 = \frac{1}{2}x - 1 \Leftrightarrow x = 2\) nên đồ thị giao với trục hoành tại \(A(2;\, 0).\) LG b \(y = 4 - 2x\) Phương pháp giải: +) Hàm số \(y=a x + b\) đồng biến trên \(R\) khi \(a >0\) và nghịch biến trên \(R\) khi \(a<0.\) Lời giải chi tiết: \(y = 4 - 2x\) Ta có: \(a=-2 < 0\) nên hàm số nghịch biến trên R. Bảng biến thiên Đồ thị hàm số: + Cho x=0 thì \(y = 4 - 2.0 = 4\) nên đồ thị giao với trục tung tại \(B(0; \,4).\) + Cho y=0 thì \(0 = 4 - 2x \Leftrightarrow x = 2\) nên đồ thị giao với trục hoành tại \(A(2; \, 0).\) LG c \(y = \sqrt {{x^2}} \) Phương pháp giải: Phá dấu giá trị tuyệt đối suy ra hàm số dưới dạng khoảng. Lập bbt và vẽ đồ thị hàm số mới thu được. Lời giải chi tiết: \(y = \sqrt {{x^2}} = |x| =\left\{ \matrix{- x \, \, \, khi \, \, x < 0 \hfill \cr x \, \, \, khi \, \, \, x \geq 0 \hfill \cr} \right.\) + Tập xác định: R + Với \(x < 0\) thì y=-x có a=-1 < 0 nên hàm số y=-x nghịch biến trên (–∞; 0). + Với \(x\ge 0\) thì y=x có a=1 > 0 nên hàm số y=x đồng biến trên (0 ; +∞). Bảng biến thiên Đồ thị hàm số: Đồ thị hàm số gồm hai phần: Phần thứ nhất: Nửa đường thẳng y = –x giữ lại phần bên trái trục tung. Phần thứ hai: Nửa đường thẳng y = x giữ lại phần bên phải trục tung.
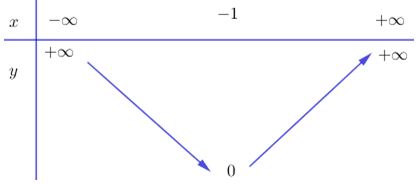
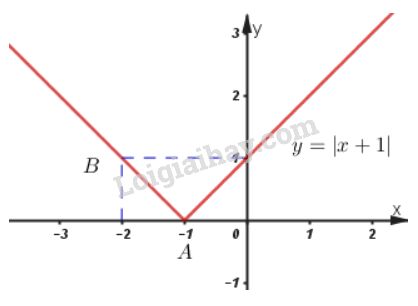
LG d \(y = |x+1|\) Phương pháp giải: Phá dấu giá trị tuyệt đối suy ra hàm số dưới dạng khoảng. Lập bbt và vẽ đồ thị hàm số mới thu được. Lời giải chi tiết: Nếu x + 1 ≥ 0 hay x ≥ –1 thì y = x + 1. Nếu x + 1 < 0 hay x < –1 thì y = –(x + 1) = –x – 1. Do đó \(y = |x+1| = \left\{ \matrix{- x - 1 \, \, \, khi x < - 1 \hfill \cr x + 1 \, \, \, khi \, \, \, x \geq - 1 \hfill \cr} \right.\) + Tập xác định: R + Trên (–1 ; +∞), y = x + 1 có a=1 > 0 nên hàm số đồng biến. + Trên (–∞; –1), y = –x – 1 có a=-1 < 0 nên hàm số nghịch biến. Bảng biến thiên Đồ thị hàm số: Đồ thị hàm số gồm hai phần: Phần thứ nhất : Nửa đường thẳng y = x + 1 giữ lại các điểm có hoành độ ≥ –1. Phần thứ hai : nửa đường thẳng y = –x – 1 giữ lại các điểm có hoành độ < –1.
Loigiaihay.com
|




















Danh sách bình luận