Bài 74 trang 17 SBT Hình học 11 Nâng cao

Đề bài

Cho điểm A cố định nằm trên đường tròn (O) và điểm C thay đổi trên đường tròn đó. Dựng hình vuông ABCD. Tìm quỹ tích điểm B và điểm D.

Lời giải chi tiết

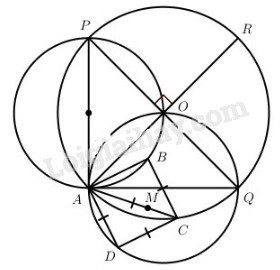
Trên đoạn thẳng AC lấy điểm M sao cho AM = AB = AD.

Khi đó, ta có \({{AM} \over {AC}} = {{AB} \over {AC}} = {{\sqrt 2 } \over 2}.\)

Ngoài ra \(\left( {AM,AB} \right) = {45^0}\) và \(\left( {AM,A{\rm{D}}} \right) =  - {45^0}\) .

Suy ra, phép vị tự V tâm A tỉ sơ \(k = {{\sqrt 2 } \over 2}\) biến điểm C thành điểm M và phép quay Q tâm A góc 45⁰ biến điểm M thành điểm B. Vậy nếu gọi F là phép hợp thành của V và Q thì F biến C thành B.

Vì quỹ tích của C là đường tròn (O), nên quỹ tích của B là ảnh của đường tròn đó qua phép đồng dạnh.

Đường tròn quỹ tích B có thể xác định như sau:

Gọi AR là đường kính của (O) và PQ là đường kính của (O) vuông góc với AR (ta kí hiệu các điểm P, Q sao cho (AR, QP = 45⁰). Khi đó dễ thấy rằng phép đồng dạng F biến AR thành AP.

Vậy quỹ tích B là đường tròn đường kính AP.

Tương tự ta được quỹ tích D là đường tròn đường kính AQ.

Loigiaihay.com