Giải bài 6 trang 26 SGK Hình học lớp 12

Đề bài

Cho hai đường thẳng chéo nhau $d$ và $d’$. Đoạn thẳng $AB$ có độ dài $a$ trượt trên $d$, đoạn thẳng $CD$ có độ dài $b$ trượt trên $d’$. Chứng minh rằng khối tứ diện $ABCD$ có thể tích không đổi.

Lời giải chi tiết

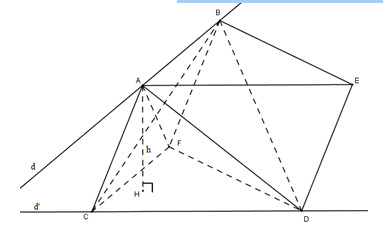
Gọi $h$ là độ dài đường vuông góc chung của $d$ và $d’$, $α$ là góc giữa hai đường thẳng $d$ và $d’$. Qua $B, A, C$ dựng hình bình hành $BACF$. Qua $A,C, D$ dựng hình bình hành $ACDE$.

Khi đó $CFD.ABE$ là một hình lăng trụ tam giác. Ta có:

$$\begin{array}{l} {V_{D.ABE}} + {V_{D.BACF}} = {V_{CFD.ABE}}\\ {V_{D.ABE}} = \dfrac{1}{3}{V_{CFD.ABE}} \Rightarrow {V_{D.BACF}} = \dfrac{2}{3}{V_{CFD.ABE}}\\ {V_{D.ABC}} = \dfrac{1}{2}{V_{D.BACF}} \Rightarrow {V_{D.ABC}} = \dfrac{1}{2}.\dfrac{2}{3}{V_{CFD.ABE}} = \dfrac{1}{3}{V_{CFD.ABE}} \end{array}$$

Kẻ $AH \bot \left( {CDF} \right)$ ta có: ${V_{ABCD}} = \dfrac{1}{3}.V_{CFD.ABE} =  \dfrac{1}{3}.AH.{S_{CDF}}$

Ta có:

$\begin{array}{l}AB//CF \Rightarrow AB//\left( {CDF} \right) \supset CD\\\Rightarrow d\left( {d;d'} \right) = d\left( {AB;CD} \right) = d\left( {AB;\left( {CDF} \right)} \right) \end{array}$

$= d\left( {A;\left( {CDF}\right)} \right) = AH = h$

$AB//CF \Rightarrow \widehat {\left( {d;d'} \right)} = \widehat {\left( {AB;CD} \right)} = \widehat {\left( {CF;CD} \right)} = \widehat {DCF} = \alpha$

$\Rightarrow {S_{CDF}} = \dfrac{1}{2}.CD.CF.\sin \widehat {DCF} = \dfrac{1}{2}ab\sin \alpha$

Vậy $V_{ABCD}=\dfrac{1}{3}.h.\dfrac{1}{2}ab\sin \alpha =\dfrac{1}{6}.h. ab. sinα = const$. (đpcm)

Loigiaihay.com