Giải bài 5 trang 26 SGK Hình học lớp 12

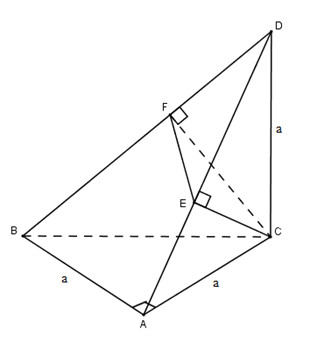
Đề bài

Cho tam giác $ABC$ vuông cân ở $A$ và $AB = a$. Trên đường thẳng qua $C$ và vuông góc với mặt phẳng $(ABC)$ lấy điểm $D$ sao cho $CD = a$. Mặt phẳng qua $C$ vuông góc với $BD$, cắt $BD$ tại $F$ và cắt $AD$ tại $E$. Tính thể tích khối tứ diện $CDEF$ theo $a$.

Lời giải chi tiết

Ta có: $BD \bot (CEF)$ hay $DF \bot (CEF)$do đó ta đã biết chiều cao của tứ diện $DCEF.$

Để tính thể tích tứ diện này, ta đi tính diện tích đáy tương ứng là ${S_{\Delta EFC}}$

Dễ thấy: $\Delta EFC$ vuông tại $E,$ vì:

$\left\{ \begin{array}{l}CE \bot DA\\CE \bot BD\;(do\;BD \bot (CEF))\end{array} \right. \Rightarrow CE \bot (BDA) \supset EF \Rightarrow CE \bot EF.$

Vậy ta đi tính các cạnh $CE, EF.$

+) Tính $CE$

Do $DC \bot (ABC)$ nên $\Delta ACD$ vuông cân tại $C.$

$\Rightarrow$ Chiều cao $CE = \dfrac{{AC}}{{\sqrt 2 }} = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }}$

+) Tính $EF$:

Xét vuông tại $C$, ta có:

$\begin{array}{l}\left\{ \begin{array}{l}DC = AC = a\\BC = AB.\sqrt 2  = a\sqrt 2 \end{array} \right. \Rightarrow BD = a\sqrt 3 \\ \text {Mà:}\;CF.BD = DC.BC\\ \Rightarrow CF = \dfrac{{DC.BC}}{{BD}} = \dfrac{{a.a\sqrt 2 }}{{a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{3}.\\ \Rightarrow EF = \sqrt {C{F^2} - C{E^2}}  = \sqrt {\dfrac{{2a}}{3} - \dfrac{a}{2}}  = \dfrac{a}{{\sqrt 6 }} = \dfrac{{a\sqrt 6 }}{6}.\end{array}$

Vậy ${S_{\Delta EFC}} = \dfrac{1}{2}CE.EF = \dfrac{1}{2}.\dfrac{a}{{\sqrt[{}]{2}}}.\dfrac{a}{{\sqrt 6 }} = \dfrac{{{a^2}}}{{4\sqrt 3 }} = \dfrac{{{a^2}\sqrt 3 }}{{12}}$

+) Chiều cao $DF$

$DF = \sqrt {D{C^2} - C{F^2}}  = \sqrt {{a^2} - \dfrac{{2{a^2}}}{3}}  = \dfrac{{a\sqrt 3 }}{3}$

Vậy ${V_{CDEF}} = \dfrac{1}{3}DF.{S_{CEF}}$ $= \dfrac{1}{3}. \dfrac{{a\sqrt 3 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{{12}} = \dfrac{{{a^3}}}{{36}}$

 

Loigiaihay.com