Bài 4 trang 155 SGK Đại số 10Rút gọn biểu thức Quảng cáo
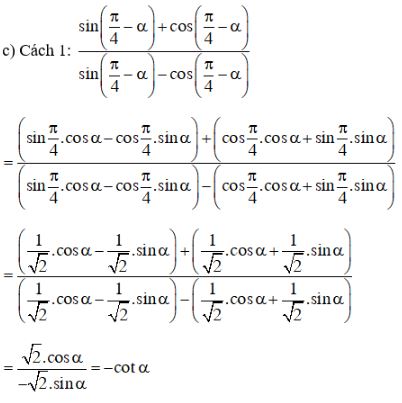
Video hướng dẫn giải Rút gọn biểu thức LG a \(\displaystyle {{2\sin 2\alpha - \sin 4\alpha } \over {2\sin 2\alpha + \sin 4\alpha }}\) Phương pháp giải: Áp dụng các công thức: \(\begin{array}{l} Lời giải chi tiết: \(\eqalign{ & {{2\sin 2\alpha - \sin 4\alpha } \over {2\sin 2\alpha + \sin 4\alpha }} \cr& = \frac{{2\sin 2\alpha - \sin \left( {2.2\alpha } \right)}}{{2\sin 2\alpha + \sin \left( {2.2\alpha } \right)}}\cr&= {{2\sin 2\alpha - 2\sin 2\alpha .cos2\alpha } \over {2\sin 2\alpha + 2\sin 2\alpha .cos2\alpha }} \cr & = \frac{{2\sin 2\alpha \left( {1 - \cos 2\alpha } \right)}}{{2\sin 2\alpha \left( {1 + \cos 2\alpha } \right)}}\cr &= {{1 - \cos 2\alpha } \over {1 + \cos 2\alpha }} = \frac{{1 - \left( {1 - 2{{\sin }^2}\alpha } \right)}}{{1 + \left( {2{{\cos }^2}\alpha - 1} \right)}}\cr&= {{2{{\sin }^2}\alpha } \over {2{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}\cr&={\left( {\frac{{\sin \alpha }}{{\cos \alpha }}} \right)^2}=\tan^2\alpha.\cr} \) LG b \(\tan \alpha ({{1 + {{\cos }^2}\alpha } \over {\sin \alpha }} - \sin \alpha )\) Lời giải chi tiết: \(\eqalign{& \tan \alpha \left({{1 + {{\cos }^2}\alpha } \over {\sin \alpha }} - \sin \alpha\right ) \cr&= {{\sin \alpha } \over {\cos \alpha }}\left({{1 + {{\cos }^2}\alpha - {{\sin }^2}\alpha } \over {\sin \alpha }}\right) \cr & = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha + {{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\sin \alpha }}\cr &= {{\sin \alpha } \over {\cos \alpha }}.{{2{{\cos }^2}\alpha } \over {\sin \alpha }} = 2\cos \alpha. \cr} \) LG c \(\displaystyle {{\sin ({\pi \over 4} - \alpha ) + \cos ({\pi \over 4} - \alpha )} \over {\sin ({\pi \over 4} - \alpha ) - \cos ({\pi \over 4} - \alpha )}}\) Lời giải chi tiết: \(\displaystyle {{\sin ({\pi \over 4} - \alpha ) + \cos ({\pi \over 4} - \alpha )} \over {\sin ({\pi \over 4} - \alpha ) - \cos ({\pi \over 4} - \alpha )}}\) \(\begin{array}{l} Cách khác: LG d \(\displaystyle {{\sin 5\alpha - \sin 3\alpha } \over {2\cos 4\alpha }}\) Lời giải chi tiết: \(\displaystyle {{\sin 5\alpha - \sin 3\alpha } \over {2\cos 4\alpha }} \) \(\displaystyle = {{2\cos {{5\alpha + 3\alpha } \over 2}\sin {{5\alpha - 3\alpha } \over 2}} \over {2\cos 4\alpha }} \) \(\displaystyle = \frac{{2\cos 4\alpha \sin \alpha }}{{2\cos 4\alpha }}\) \(\displaystyle = \sin \alpha \) Loigiaihay.com
|














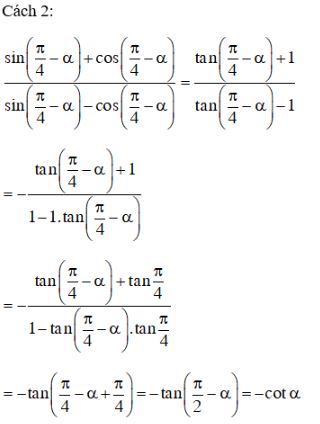







Danh sách bình luận