Bài 28 trang 9 SBT Hình Học 11 nâng cao

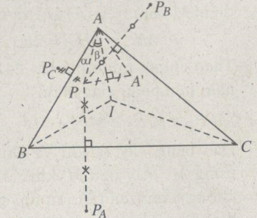
Đề bài

Cho tam giác ABC với I là tâm đường tròn nội tiếp và P là điểm nằm trong tam giác. Gọi A’, B’, C’ là các điểm đối xứng với điểm P lần lượt qua các đường thẳng AI, BI, CI. Chứng minh rằng các đường thẳng AA’, BB’, CC’ đồng quy.

Lời giải chi tiết

Ta xét trường hợp P nằm trong góc BAI.

Gọi \({P_A},\,{P_B},\,{P_C}\) là các điểm đối xứng với P lần lượt qua các đường thẳng BC, CA, AB.

Ta chứng minh rằng AA’ là đường trung trực của đoạn thẳng \({P_B}{P_{C}}\).

Thật vậy, nếu ta kí kiệu \(\widehat {PAB} = \alpha ,\,\widehat {PAI} = \beta \), ta có:

\(\widehat {{P_C}AA'} = \widehat {{P_C}AP} + \widehat {PAA'} = 2\alpha  + 2\beta \)

Và

\(\eqalign{
& \widehat {A'A{P_B}} = \widehat {A'AC} + \widehat {CA{P_B}} \cr 
& = \widehat {A'AC} + \widehat {CAP} = \alpha + \alpha + 2\beta \cr 
& = 2\alpha + 2\beta . \cr} \)

Vậy \(\widehat {{P_C}AA'} = \widehat {A'A{P_B}}\)

Ngoài ra, hiển nhiên \(A{P_C} = A{P_B}.\)

Suy ra AA’ là đường trung trực của đoạn thẳng \({P_B}{P_C}.\)

Chứng minh tương tự, ta cũng có BB’ là đường trung trực của đoạn thẳng \({P_C}{P_A}\) và CC’ là đường trung trực của đoạn thẳng \({P_C}{P_A}\) và CC’ là đường trung trực của đoạn thẳng \({P_A}{P_B}.\)

Suy ra AA’, BB’, CC’ đồng quy tại tâm đường tròn ngoại tiếp tam giác \({P_A}{P_B}{P_C}.\)

Trường hợp P nằm trong góc CAI, lập luận tương tự.

Loigiaihay.com