Câu 28 trang 112 SGK Hình học 11 Nâng caoCho tam giác ABC và mặt phẳng (P). Biết góc giữa mp(P) và mp(ABC) là φ (φ ≠ 90˚); hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
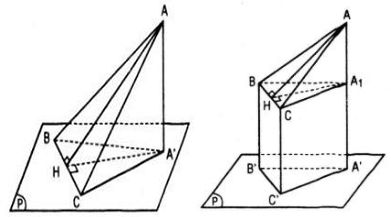
Cho tam giác ABC và mặt phẳng (P). Biết góc giữa mp(P) và mp(ABC) là φ (φ ≠ 90˚); hình chiếu của tam giác ABC trên mp(P) là tam giác A’B’C’. Chứng minh rằng \({S_{A'B'C'}} = {S_{ABC}}.\cos \varphi \) Hướng dẫn. Xét hai trường hợp : a) Tam giác ABC có 1 cạnh song song hoặc nằm trong mp(P). b) Tam giác ABC không có cạnh nào song song hay nằm trong mp(P). LG a Tam giác ABC có một cạnh song song hoặc nằm trong mp(P) Lời giải chi tiết: Xét trường hợp tam giác ABC có một cạnh, chẳng hạn BC nằm trong mp(P). Gọi A’ là hình chiếu của A trên mp(P). Kẻ đường cao A’H của tam giác A’BC (H ϵ BC) thì AH là đường cao của tam giác ABC và \(\widehat {AHA'} = \varphi ,A'H = AH\cos \varphi .\) Ta có: \({S_{A'BC}} = {1 \over 2}BC.A'H \) \(= {1 \over 2}BC.AH\cos \varphi = {S_{ABC.cos\varphi }}\)
Trường hợp cạnh BC của tam giác ABC song song với mp(P). Xét mp(Q) chứa BC và song song với mp(P), gọi giao điểm của AA’ với mp(Q) là A1. Khi đó ta có ΔA1BC = ΔA’B’C’ ; góc giữa mp(ABC) và mp(Q) bằng φ. Do đó : \({S_{A'B'C'}} = {S_{{A_1}BC}} = {S_{ABC }.\cos \varphi}\) LG b Tam giác ABC không có cạnh nào song song hay nằm trong mp(P). Lời giải chi tiết:
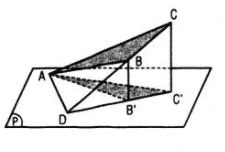
Xét trường hợp tam giác ABC không có cạnh nào song song hay nằm trong mp(P). Ta có thể giả sử mp(P) đi qua điểm A sao cho các đỉnh B, C ở về cùng một phía đối với mp(P). Gọi D là giao điểm của đường thẳng BC và mp(P); B’, C’ lần lượt là hình chiếu của B, C trên (P) thì B’C’ đi qua D. Khi đó theo trường hợp a ta có : \(\eqalign{ & {S_{ADC'}} = {S_{ADC.\cos \varphi }} \cr & {S_{ADB'}} = {S_{ABD.\cos \varphi }} \cr} \) Trừ từng vế hai đẳng thức trên, ta có : \({S_{AB'C'}} = {S_{ABC.\cos \varphi }}\) Vậy mọi trường hợp ta đều có : \({S_{A'B'C'}} = {S_{ABC.\cos \varphi }}\) Loigiaihay.com
|




















Danh sách bình luận