Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học

Câu 25 trang 32 SGK Đại số và Giải tích 11 Nâng cao

Một chiếc guồng nước có dạng hình tròn bán kính 2,5m ; trục của nó đặt cách mặt nước 2m

Quảng cáo

Lựa chọn câu để xem lời giải nhanh hơn

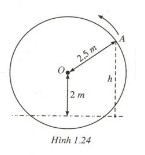
Một chiếc guồng nước có dạng hình tròn bán kính \(2,5m\) ;trục của nó đặt cách mặt nước \(2m\) (h.1.24). Khi guồng quay đều, khoảng cách \(h\) (mét) từ một chiếc gầu gắntại điểm \(A\) của guồng đến mặt nước được tính theo công thức \(h = |y|\), trong đó

\(y = 2 + 2,5\sin \left[ {2\pi \left( {x - {1 \over 4}} \right)} \right]\)

Với \(x\) là thời gian quay guồng (\(x ≥ 0\)), tính bằng phút ; ta quy ước rằng \(y > 0\) khi gầu ở bên trên mặt nước và \(y < 0\) khi gầu ở dưới nước (xem bài đọc thêm về dao động điều hòa trang 15). Hỏi :

LG a

Khi nào thì chiếc gầu ở vị trí thấp nhất ?

Lời giải chi tiết:

Ta có: \(\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] \ge - 1\) \( \Rightarrow y \ge 2 + 2,5.\left( { - 1} \right) = - 0,5\)

Chiếc gầu ở vị trí thấp nhất khi \(\sin \left[ {2\pi \left( {x - {1 \over 4}} \right)} \right] = - 1.\) Ta có :

\(\sin \left[ {2\pi \left( {x - {1 \over 4}} \right)} \right] = - 1 \)

\(\Leftrightarrow 2\pi \left( {x - {1 \over 4}} \right) = - {\pi \over 2} + k2\pi \)

\( \Leftrightarrow x - \frac{1}{4} = - \frac{1}{4} + k\)

\(\Leftrightarrow x = k\,\left( {\,k \in\mathbb Z} \right)\)

Điều đó chứng tỏ rằng chiếc gầu ở vị trí thấp nhất tại các thời điểm 0 phút ; 1 phút ; 2 phút ; 3 phút…

LG b

Khi nào thì chiếc gầu ở vị trí cao nhất ?

Lời giải chi tiết:

Ta có: \(\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] \le 1\) \( \Rightarrow y \le 2 + 2,5.1 = 4,5\)

Chiếc gầu ở vị trí cao nhất khi \(\sin \left[ {2\pi \left( {x - {1 \over 4}} \right)} \right] = 1.\) Ta có :

\(\sin \left[ {2\pi \left( {x - {1 \over 4}} \right)} \right] = 1\)

\(\Leftrightarrow 2\pi \left( {x - {1 \over 4}} \right) = {\pi \over 2} + k2\pi\)

\( \Leftrightarrow x - \frac{1}{4} = \frac{1}{4} + k\)

\(\Leftrightarrow x = {1 \over 2} + k\,\left( {\,k \in N} \right)\)

Điều đó chứng tỏ chiếc gàu ở vị trí cao nhất tại các thời điểm 0,5 phút; 1,5 phút ; 2,5 phút ; 3,5 phút …

LG c

Chiếc gầu cách mặt nước \(2m\) lần đầu tiên khi nào ?

Lời giải chi tiết:

Chiếc gàu cách mặt nước 2 mét khi:

\(\begin{array}{l}
2 + 2,5\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] = 2\\
\Leftrightarrow 2,5\sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] = 0\\
\Leftrightarrow \sin \left[ {2\pi \left( {x - \frac{1}{4}} \right)} \right] = 0\\
\Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = k\pi \\
\Leftrightarrow x - \frac{1}{4} = \frac{k}{2}\\
\Leftrightarrow x = \frac{k}{2} + \frac{1}{4}
\end{array}\)

Nghĩa là tại các thời điểm \(x = {1 \over 4} + {1 \over 2}k\) (phút) thì chiếc gầu cách mặt nước 2m;

Do đó lần đầu tiên nó cách mặt nước 2 mét khi quay được \({1 \over 4}\) phút (ứng với \(k = 0\)).

Loigiaihay.com