Câu 2 trang 34 SGK Hình học 11 Nâng caoChứng minh rằng nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng Quảng cáo
Đề bài Chứng minh rằng nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng Lời giải chi tiết
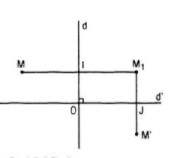
Giả sử hình H có hai trục đối xứng d và d’ vuông góc với nhau Gọi O là giao điểm của hai trục đối xứng đó Lấy M là điểm bất kì thuộc hình H, M1 là điểm đối xứng với M qua d, M’ là điểm đối xứng với M1 qua d’ Vì d và d’ đều là trục đối xứng của hình H nên M1 và M’ đều thuộc H Gọi I là trung điểm của MM1, J là trung điểm của M1M’ thì ta có: \(\overrightarrow {OM} = \overrightarrow {OI} + \overrightarrow {IM} = \overrightarrow {M'J} + \overrightarrow {JO} = \overrightarrow {M'O} \) hay \(\overrightarrow {OM} + \overrightarrow {OM'} = \overrightarrow 0 \) Vậy phép đối xứng tâm O biến điểm M thuộc hình H thành điểm M’ thuộc H, suy ra H có tâm đối xứng là O Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
