Bài 1.58 trang 22 SBT Giải tích 12 Nâng cao

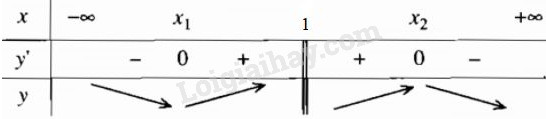
LG a

Tìm các giá trị m sao cho hàm số

\(y = {{ - 2{x^2} + (m + 2)x - 3m + 1} \over {x - 1}}\)

Nghịch biến trên mỗi khoảng xác định của nó.

Lời giải chi tiết:

Ta viết hàm số đã cho dưới dạng

\(y =  - 2x + m + {{1 - 2m} \over {x - 1}}\)

Khi đó: \(y' =  - 2 + {{2m - 1} \over {{{(x - 1)}^2}}}\)

+) Nếu \(2m - 1 \le 0\) hay \(m \le {1 \over 2}\) thì \(y' < 0\) với mọi \(x \ne 1\).

Do đó hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)

+) Dễ thấy nếu \(2m - 1 > 0\) hay \(m > {1 \over 2}\) thì phương trình \(y' = 0\) có hai nghiệm \({x_1},{x_2}\) trong đó \({x_1} < 1 < {x_2}\)

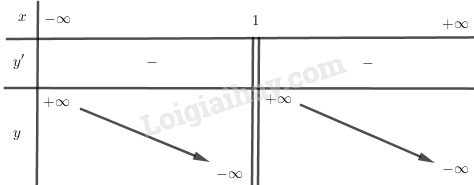
Hàm số đồng biến trên mỗi khoảng \(\left( {{x_1};1} \right)\) và \(\left( {1;{x_2}} \right)\).

Trong trường hợp này, các giá trị của m không thỏa mãn điều kiện đòi hỏi.

LG b

Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 0.

Lời giải chi tiết:

Với \(m = 0\) ta được \(y = \frac{{ - 2{x^2} + 2x + 1}}{{x - 1}} =  - 2x + \frac{1}{{x - 1}}\)

+) TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)

+) Chiều biến thiên:

\(\mathop {\lim }\limits_{x \to {1^ + }} y =  + \infty ,\mathop {\lim }\limits_{x \to {1^ - }} y =  - \infty \) nên TCĐ: \(x = 1\).

\(\mathop {\lim }\limits_{x \to  \pm \infty } \left( {y + 2x} \right) = \mathop {\lim }\limits_{x \to  \pm \infty } \left( {\frac{1}{{x - 1}}} \right) = 0\) nên TCX: \(y = x - 1\).

Ta có:

\(y' =  - 2 - \frac{1}{{{{\left( {x - 1} \right)}^2}}} < 0,\forall x \in D\)

Hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) và không có cực trị.

BBT:

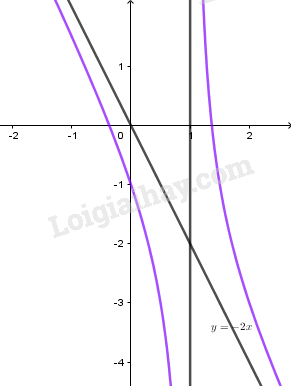
+) Đồ thị:

Loigiaihay.com