Bài 1.52 trang 20 SBT Giải tích 12 Nâng cao

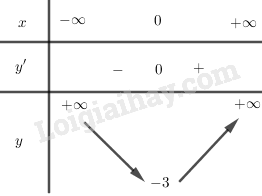
LG a

Khảo sát sự biến thiên và vẽ đồ thị  của hàm số

\(y = {x^4} + {x^2} - 3\)

Lời giải chi tiết:

+) TXĐ: \(D = \mathbb{R}\).

+) Chiều biến thiên:

\(\mathop {\lim }\limits_{x \to  \pm \infty } y =  + \infty \)

\(\begin{array}{l}y' = 4{x^3} + 2x\\y' = 0 \Leftrightarrow 4{x^3} + 2x = 0\\ \Leftrightarrow 2x\left( {2{x^2} + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\2{x^2} + 1 = 0\left( {VN} \right)\end{array} \right.\\ \Leftrightarrow x = 0\end{array}\)

BBT:

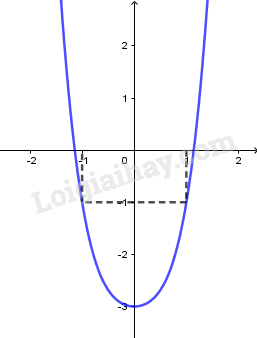
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).

Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\).

Hàm số đạt cực tiểu tại \(x = 0,{y_{CT}} =  - 3\).

+) Đồ thị:

Trục đối xứng: \(Oy\).

Đồ thị hàm số cắt trục tung tại điểm \(\left( {0; - 3} \right)\), đi qua các điểm \(\left( {1; - 1} \right),\left( { - 1; - 1} \right)\)

LG b

Chứng minh rằng đường thẳng \(y =  - 6x - 7\) tiếp xúc với đồ thị của hàm số đã cho tại điểm có hoành độ bằng \( - 1\).

Lời giải chi tiết:

Với \(x =  - 1\) ta có \(y\left( { - 1} \right) =  - 1\).

\(y'\left( { - 1} \right) = 4.{\left( { - 1} \right)^3} + 2.\left( { - 1} \right) =  - 6\)

Tiếp tuyến với đồ thị tại \(\left( { - 1; - 1} \right)\) là:

\(y =  - 6\left( {x + 1} \right) - 1\) hay \(y =  - 6x - 7\)

Vậy đường thẳng \(y =  - 6x - 7\) là tiếp tuyến của đồ thị tại điểm \(\left( { - 1; - 1} \right)\) hay đường thẳng \(y =  - 6x - 7\) tiếp xúc với đồ thị của hàm số đã cho tại điểm có hoành độ bằng \( - 1\) (đpcm)

Loigiaihay.com