Bài 1.13 trang 9 SBT Đại số và Giải tích 11 Nâng cao

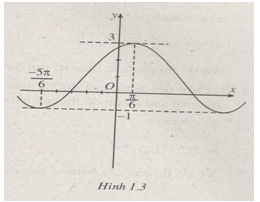
Đề bài

Cho biết đồ thị (h.1.3) sau là đồ thị hàm số \(y = A\sin \left( {x + \alpha } \right) + B\) (\(A,B,\alpha \) là những hằng số). Hãy xác định \(A,B,\alpha \).

 

Lời giải chi tiết

Hàm số \(y = A\sin \left( {x + \alpha } \right) + B\) đạt giá trị lớn nhất là 3 tại \(x = {\pi  \over 6}\) (coi \(A > 0\)) nên:

\(\left\{ \matrix{
\sin \left( {{\pi \over 6} + \alpha } \right) = 1 \hfill \cr 
A + B = 3 \hfill \cr} \right.\)

Hàm số  \(y = A\sin \left( {x + \alpha } \right) + B\) đạt giá trị nhỏ nhất là -1 tại \(x =  - {{5\pi } \over 6}\) nên:

\(\left\{ \matrix{
\sin \left( { - {{5\pi } \over 6} + \alpha } \right) = - 1 \hfill \cr 
- A + B = - 1 \hfill \cr} \right.\)

Từ đó \(B = 1,A = 2\) và chú ý rằng

\(\sin \left( { - {{5\pi } \over 6} + \alpha } \right) = \sin \left( {{\pi  \over 6} + \alpha  - \pi } \right)\) \( = \sin \left( {{\pi  \over 6} + \alpha } \right)\)

Nên chỉ cần chọn \(\alpha \) sao cho \(\left( {{\pi  \over 6} + \alpha } \right) = 1,\) chẳng hạn \(\alpha  = {\pi  \over 3}\)

Vậy \(A = 2,B = 1,\alpha  = {\pi  \over 3}\)

Loigiaihay.com