Câu 1 trang 124 SGK Hình học 11 Nâng cao

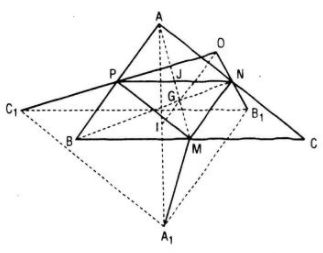
Đề bài

Cho tam giác ABC và các điểm M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.

a. Xét bốn tam giác APN, PBM, NMC, MNP. Tìm phép dời hình biến tam giác APN lần lượt thành một trong ba tam giác còn lại.

b. Phép vị tự nào biến tam giác ABC thành tam giác MNP ?

c. Xét tam giác có ba đỉnh là trực tâm của ba tam giác APN, PBM và NCM. Chứng tỏ rằng tam giác đó bằng tam giác APN. Chứng minh điều đó cũng đúng nếu thay trực tâm bằng trọng tâm, hoặc tâm đường tròn ngoại tiếp hoặc tâm đường tròn nội tiếp. 

Quảng cáo

Lời giải chi tiết

a. Phép tịnh tiến ${T_{\overrightarrow {AP} }}$ biến tam giác APN thành tam giác PBM.

Phép tịnh tiến ${T_{\overrightarrow {AN} }}$ biến tam giác APN thành tam giác NMC. Phép đối xứng tâm Đ­_J, với J là trung điểm của PN, biến tam giác APN thành tam giác MNP.

b. Gọi G là trọng tâm của tam giác ABC thì $\overrightarrow {GM}  =  - {1 \over 2}\overrightarrow {GA} ,\overrightarrow {GN}  =  - {1 \over 2}\overrightarrow {GB} ,\overrightarrow {GP}  =  - {1 \over 2}\overrightarrow {GC} .$

Vậy phép vị tự tâm G, tỉ số $k =  - {1 \over 2}$ biến tam giác ABC thành tam giác MNP.

c. Gọi H₁, H₂, H₃ lần lượt là trực tâm của tam giác APN, PBM, NMC.

Phép tịnh tiến ${T_{\overrightarrow {AP} }}$ biến APN thành tam giác PBM nên biến H₁ thành H₂, tức là $\overrightarrow {{H_1}{H_2}}  = \overrightarrow {AP} \,hay\,\overrightarrow {A{H_1}}  = \overrightarrow {P{H_2}} .$ Tương tự ta có $\overrightarrow {{H_1}{H_3}}  = \overrightarrow {AN} \,hay\,\overrightarrow {A{H_1}}  = \overrightarrow {N{H_3}} .$

Vậy $\overrightarrow {A{H_1}}  = \overrightarrow {P{H_2}}  = \overrightarrow {N{H_3}} .$ Từ đó suy ra phép tịnh tiến theo vecto $\overrightarrow {A{H_1}}$ biến tam giác APN thành tam giác H₁H₂H₃.

Đối với các trường hợp khác (trọng tâm, tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếp), chứng minh hoàn toàn tương tự.

Loigiaihay.com