Bài tập 8 trang 134 Tài liệu dạy – học Toán 8 tập 1Giải bài tập Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Quảng cáo
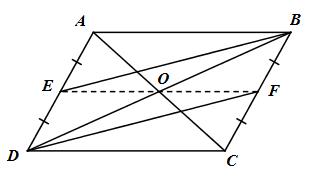
Đề bài Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. a) Chứng minh tứ giác EBFD là hình bình hành. b) Gọi O là tâm đối xứng của hình bình hành ABCD. CHứng minh rằng ba điểm E, O, F thẳng hàng. Lời giải chi tiết
a) Ta có : \(ED = {1 \over 2}AD\) (E là trung điểm của AD) \(BF = {1 \over 2}BC\) (F là trung điểm của BC) Và \(AD = BC\) (ABCD là hình bình hành) \( \Rightarrow ED = BF\) Mà ED // BF (AD // BC, \(E \in AD;\,\,F \in BC\)) Do đó tứ giác EBFD là hình bình hành. b) O là tâm đối xứng của hình bình hành ABCD \( \Rightarrow O\) là trung điểm của BD Hình bình hành EBFD có O là trung điểm của BD \( \Rightarrow O\) là trung điểm của EF. \( \Rightarrow O \in EF\). Vậy E, O, F thẳng hàng. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
