Bài tập 7 trang 134 Tài liệu dạy – học Toán 8 tập 1Giải bài tập Cho hình 61, trong đó ABCD là hình bình hành. Quảng cáo
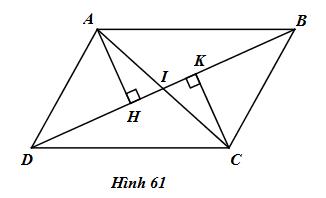
Đề bài Cho hình 61, trong đó ABCD là hình bình hành. a) Chứng minh rằng tứ giác AHCK là hình bình hành. b) Gọi I là trung điểm của BD. Chứng minh rằng ba điểm A, I, C thẳng hàng.
Lời giải chi tiết a) Xét \(\Delta ADH\,\,\left( {\widehat H = {{90}^0}} \right)\) và \(\Delta KBC\,\,\left( {\widehat K = {{90}^0}} \right)\) có: \(AD = BC\) (ABCD là hình bình hành) \(\widehat {ADH} = \widehat {KBC}\) (hai góc so le trong và \(AD // BC\)) Do đó \(\Delta ADH = \Delta CBK\) (cạnh huyền – góc nhọn) \( \Rightarrow AH = CK\) Mà AH // CK (cùng vuông góc với DB) \( \Rightarrow \) Tứ giác AHCK là hình bình hành b) Hình bình hành ABCD có I là trung điểm của BD nên I là trung điểm của AC \( \Rightarrow A,I,C\) thẳng hàng. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
