Bài tập 23 trang 136 Tài liệu dạy – học Toán 8 tập 1Giải bài tập Cho tam giác ABC vuông tại A. Lấy M là điểm bất kì trên cạnh BC. Gọi E, F lần lượt là chân các đường vuông góc kẻ từ M đến AB, AC. Quảng cáo
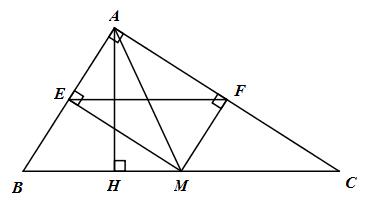
Đề bài Cho tam giác ABC vuông tại A. Lấy M là điểm bất kì trên cạnh BC. Gọi E, F lần lượt là chân các đường vuông góc kẻ từ M đến AB, AC. a) Chứng minh rằng AM = EF. b) Điểm M ở vị trí nào trên cạnh BC thì AM có độ dài nhỏ nhất ? Lời giải chi tiết
a) Tứ giác AEMF có: \(\widehat {EAF} = {90^0}\) (\(\Delta ABC\) vuông tại A) \(\widehat {AFM} = {90^0}\,\,\,\left( {FM \bot AC} \right)\) \(\widehat {AEM} = {90^0}\,\,\left( {EM \bot AB} \right)\) \( \Rightarrow \) Tứ giác AEMF là hình chữ nhật \( \Rightarrow AM = EF\). b) Kẻ \(AH \bot BC\) tại H, ta có H cố định. Ta có \(AM \ge AH\) (\(AH \bot BC\) tại H, \(M \in BC\)) Dấu “=” xảy ra \( \Leftrightarrow M \equiv H\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
