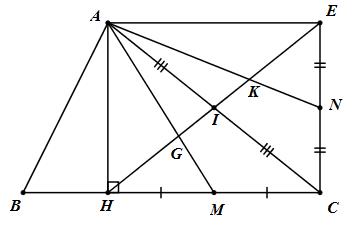
Bài tập 17 trang 135 Tài liệu dạy – học Toán 8 tập 1

Đề bài

Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm dối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.

a) Chứng minh tứ giác AHCE là hình chữ nhật.

b) Chứng minh HG = GK = KE.

Lời giải chi tiết

a) Tứ giác AHCE có hai đường chéo AC và HE cắt nhau tại I (gt)

I là trung điểm của AC (gt);

Và I là trung điểm của HE (E đối xứng với H qua I)

Do đó tứ giác AHCE là hình bình hành.

Mà \(\widehat {AHC} = {90^0}\)  (AH là đường cao của tam giác ABC)

Vậy tứ giác AHCE là hình chữ nhật.

b) \(MAHC\) có: HI là đường trung tuyến (I là trung điểm của AC)

Và AM là đường trung tuyến (M là trung điểm của HC)

Mà HI cắt AM tại G (gt)

Do đó G là trọng tâm của tam giác AHC \( \Rightarrow HG = {2 \over 3}HI\) và \(GI = {1 \over 3}HI\,\,\left( 1 \right)\)

\(\Delta AEC\) có hai đường trung tuyến AN và EI cắt nhau tại K.

\( \Rightarrow K\) là trọng tâm của tam giác AEC \( \Rightarrow KE = {2 \over 3}IE\) và \(KI = {1 \over 3}IE\,\,\left( 2 \right)\)

\(HI = IE\) (E đối xứng với H qua I)  (3)

Từ (1), (2) và (3) suy ra \(HG = KE = {2 \over 3}IE\).

Ta có: \(GK = GI + IK = {1 \over 3}IE + {1 \over 3}IE = {2 \over 3}IE \Rightarrow HG = KE = GK\left( { = {2 \over 3}IE} \right)\)

Loigiaihay.com