Bài tập 12 trang 69 Tài liệu dạy – học Toán 8 tập 2

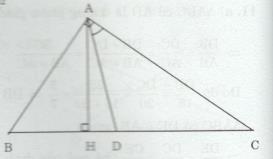
Đề bài

Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Đường phân giác cảu góc A cắt BC tại D.

a) Tính BC, DB, DC

b) Vẽ đường cao AH. Tính AH, HD và AD.

Lời giải chi tiết

a) ∆ABC vuông tại A có $B{C^2} = A{B^2} + A{C^2}$ (định lý Py-ta-go)

$\Rightarrow B{C^2} = {3^2} + {4^2} = 25$

$\Rightarrow BC = 5(cm)$

Xét ∆ABC có AD là đường phân giác (gt)

$\eqalign{  &  \Rightarrow {{DB} \over {DC}} = {{AB} \over {AC}} = {3 \over 4}\cr& \Rightarrow {{DB} \over 3} = {{DC} \over 4}  \cr  &  \Leftrightarrow {{DB} \over 3} = {{DC} \over 4} = {{DB + DC} \over {3 + 4}} = {{BC} \over 7} = {5 \over 7} \cr}$

Do vậy $DB = {5 \over 7}.3 = {{15} \over 7}(cm)$ và $DC = {5 \over 7}.4 = {{20} \over 7}(cm)$

b) Ta có ${S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}.3.4 = 6$ và ${S_{ABC}} = {1 \over 2}AH.BC$

$\Rightarrow 6 = {1 \over 2}AH.BC$

$\Rightarrow 6 = {1 \over 2}AH.5$

$\Rightarrow AH = {{12} \over 5} = 2,4(cm)$

∆ABH vuông tại H có $B{H^2} + A{H^2} = A{B^2}$ (định lý Py-ta-go)

$\eqalign{  &  \Rightarrow B{H^2} + 2,{4^2} = {3^2}\cr& \Rightarrow B{H^2} = 3,24 = 1,{8^2} \cr&\Rightarrow BH = 1,8(cm)  \cr  & HD = DB - BH = {{15} \over 7} - 1,8 \cr&\;\;\;\;\;\;\;\;= {{15} \over 7} - {9 \over 5} = {{12} \over {35}}(cm) \cr}$

∆AHD vuông tại H có $A{D^2} = H{D^2} + A{H^2}$ (định lý Py-ta-go)

$\Rightarrow A{D^2} = {\left( {{{12} \over {35}}} \right)^2} + 2,{4^2}$$\,= {{144} \over {1225}} + {{144} \over {25}} = {{288} \over {49}}$

Mà $AD > 0 \Rightarrow AD = \sqrt {{{288} \over {49}}} (cm)$

Loigiaihay.com