Bài 9 trang 101 SGK Toán 9 tập 1Vẽ lại hình. Quảng cáo
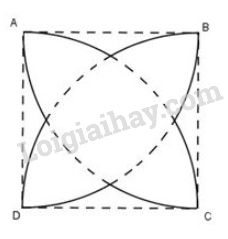
Đề bài a) Vẽ hình hoa bốn cánh. Hình hoa bốn cánh trên hình \(60\) được tạo ra bởi các cung có tâm \(A,\ B,\ C,\ D\) (trong đó \(A,\ B,\ C,\ D\) là các đỉnh của một hình vuông và tâm của cung là tâm của đường tròn chứa cung đó). Hãy vẽ lại hình \(60\) vào vở.
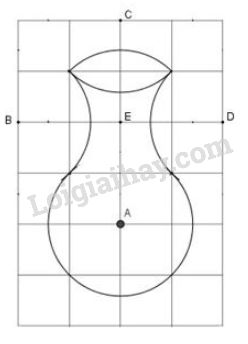
b) Vẽ lọ hoa: Chiếc lọ hoa trên hình \(61\) được vẽ trên giấy kẻ ô vuông bởi năm cung có tâm \(A,\ B,\ C,\ D,\ E\). Hãy vẽ lại hình \(61\) vào giấy kẻ ô vuông.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Sử dụng định lí Pytago để tính độ dài các đường chéo của hình vuông có cạnh là \(1cm\). Lời giải chi tiết a) - Vẽ hình vuông \(ABCD\). - Vẽ 4 cung tròn tâm \(A, B, C, D\) bán kính \(AB\). Ta được bốn cung tròn tạo thành hình hoa bốn cánh. b) Đường chéo hình vuông có cạnh là 1 có độ dài là \(\sqrt {1^2+1^2}=\sqrt 2.\) - Kẻ lại các ô vuông và lấy các điểm như hình 61. - Vẽ 5 cung tròn tâm \(A,B,C,D,E\) bán kính \(\sqrt 2\). Ta được năm cung tròn liền nét với nhau tạo thành hình chiếc lọ hoa.
|




















Danh sách bình luận