Bài 89 trang 118 SBT Hình học 10 Nâng cao

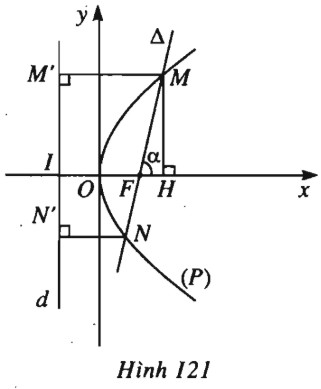
Đề bài

Cho parabol \((P): {y^2} = 2px  (p > 0)\) và đường thẳng \(\Delta \) đi qua tiêu điểm \(F\) của \((P)\) và cắt \((P)\) tại hai điểm \(M\) và \(N\). Gọi \(\alpha  = \left( {\overrightarrow i  , \overrightarrow {FM} } \right) (0 < \alpha  < \pi )\).

a) Tính \(FM, FN\) theo \(p\) và \(\alpha \).

b) Chứng minh rằng khi \(\Delta \) quay quanh \(F\) thì \( \dfrac{1}{{FM}} +  \dfrac{1}{{FN}}\) không đổi.

c) Tìm giá trị nhỏ nhất của tích \(FM.FN\) khi \(\alpha \) thay đổi.

Lời giải chi tiết

(h.121).

Gọi \(H, M’\) thứ tự là hình chiếu của \(M\) trên \(Ox\) và đường chuẩn \(d\) cả parabol \((P)\), còn \(I\) là giao điểm của \(Ox\) và \(d\). Ta có

\(\begin{array}{l}MF = MM' = IH.\\\overline {IH}  = \overline {IF}  + \overline {FH}\\     \Rightarrow    IH = p + \overrightarrow {FM} .\overrightarrow i \\= p + MF\cos \alpha \\ \Rightarrow   MF =  \dfrac{p}{{1 - \cos \alpha }}.\end{array}\)

Do \(\left( {\overrightarrow {FN} , \overrightarrow i } \right) = {180^0} - \alpha \) nên tương tự như trên ta cũng có

\(NF =  \dfrac{p}{{1 - \cos ({{180}^0} - \alpha )}}\)

\(=  \dfrac{p}{{1 + \cos \alpha }}\)

b) \( \dfrac{1}{{FM}} +  \dfrac{1}{{FN}} \)

\(=  \dfrac{{1 - \cos \alpha }}{p} +  \dfrac{{1 + \cos \alpha }}{p}\)

\(=  \dfrac{2}{p}\) không đổi.

c) \(FM.FN \)

\(=  \dfrac{p}{{1 - \cos \alpha }}. \dfrac{p}{{1 + \cos \alpha }}\)

\(=  \dfrac{{{p^2}}}{{1 - {{\cos }^2}\alpha }} \)

\(=  \dfrac{{{p^2}}}{{{{\sin }^2}\alpha }}\)

\(FM.FN\) có giá trị nhỏ nhất \( \Leftrightarrow     {\sin ^2}\alpha \) lớn  nhất \( \Leftrightarrow \sin \alpha  = 1   \Leftrightarrow \Delta  \bot Ox\).

Loigiaihay.com