Bài 8.45 trang 90 SGK Toán 11 tập 2 - Cùng khám phá

Đề bài

Cho tử diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC. Gọi M là trung điểm của BC. Góc giữa hai đường thẳng OM và AB bằng

A. 90⁰.

B. 30⁰.

C. 60⁰.

D. 45⁰.

Lời giải chi tiết

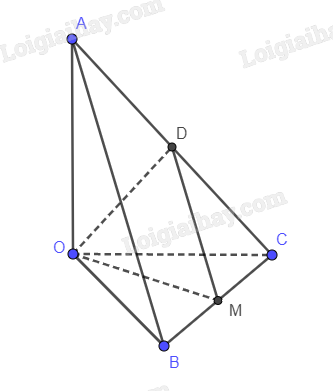
Đặt OA = OB = OC = a

Gọi D là trung điểm của AC nên DM // AB và bằng một nửa AB

\( \Rightarrow \widehat {\left( {OM,AB} \right)} = \widehat {\left( {OM,DM} \right)} = \widehat {OMD}\)

Ta có: OA vuông góc và bằng OC nên tam giác OAC là tam giác vuông cân tại C

\(AC = \sqrt {O{A^2} + O{B^2}}  = \sqrt 2 a\)

\(\begin{array}{l}AC.OD = OA.OC\\ \Leftrightarrow OD = \frac{{\sqrt 2 }}{2}a\end{array}\)

Tương tự với OM, ta có: \(OM = \frac{{\sqrt 2 }}{2}a\)

\(AB = \sqrt {O{A^2} + O{B^2}}  = \sqrt 2 a\)

Suy ra \(DM = \frac{{\sqrt 2 }}{2}a\)

Vậy tam giác DOM đều. Suy ra \(\widehat {OMD} = {60^0}\).

Chọn đáp án C.