Bài 8 trang 45 SGK Đại số 10 nâng caoGiả sử (G) là đồ thị của hàm số y = f(x) xác định trên tập D và A là một điểm trên trục hoành có hoành độ bằng a. Từ A, ta dựng đường thẳng (d) song song (hoặc trùng) với trục tung. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
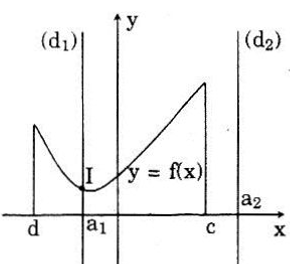
Giả sử (G) là đồ thị của hàm số y = f(x) xác định trên tập D và A là một điểm trên trục hoành có hoành độ bằng a. Từ A, ta dựng đường thẳng (d) song song (hoặc trùng) với trục tung. LG a Khi nào thì (d) có điểm chung với (G)? (Hướng dẫn: Xét hai trường hợp a thuộc D và a không thuộc D) Phương pháp giải: Vẽ hình minh họa trong hai trường hợp \(a\in D\) và \(a\notin D\) để suy ra d và (G) có giao điểm hay không. Lời giải chi tiết: Hình vẽ bên minh họa cho trường hợp D = (d; c). Ở đó, đồ thị (G) là đường cong trong hình, các đường thẳng \(d_1,d_2\) là các đường thẳng song song hoặc trùng Oy, đi qua điểm \(A_1(a_1;0),A_2(a_2;0)\). Trường hợp a = a1 ∈ D, ta có (d1) có giao điểm với (G) tại I.
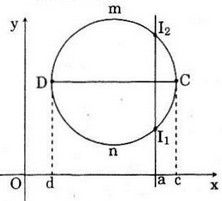
Trường hợp a = a2 ∉ D thì (d2) và (G) không có giao điểm. Vậy, - (d) và (G) có điểm chung khi a ∈ D. - (d) và (G) không có điểm chung khi a ∉ D. LG b (d) có thể có bao nhiêu điểm chung với (G)? Vì sao? Lời giải chi tiết: (d) và (G) có không quá một điểm chung, vì nếu trái lại, gọi M1 và M2 là hai điểm chung phân biệt thì ứng với a có tới hai giá trị của hàm số là các tung độ của điểm M1, M2. Trái với định nghĩa của hàm số. LG c Đường tròn có thể là đồ thị của hàm số nào không? Vì sao? Lời giải chi tiết: Đường tròn không thể là đồ thị của một hàm số vì đường thẳng song song với Oy cắt đường tròn tại hai điểm phân biệt.
Chú ý: Đường tròn có thể coi là sự hợp bởi hai đồ thị hàm số. Ở hình trên ta có thể xem đường tròn là sự hợp bởi hai đồ thị hàm số nên đồ thị (G1) là cung DmC và đồ thị (G2) là cung DnC. Loigiaihay.com
|




















Danh sách bình luận