Bài 8 trang 119 Tài liệu dạy – học Toán 9 tập 1

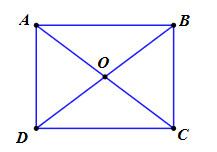
Đề bài

Cho hình chữ nhật ABCD có AD = 18 cm, CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Lời giải chi tiết

 

Gọi \(O = AC \cap BD\).

Do \(ABCD\) là hình chữ nhật, do đó hai đường chéo \(AC\) và \(BD\) bằng nhau và cắt nhau tại trung điểm mỗi đường \( \Rightarrow OA = OB = OC = OD\).

Vậy bốn điểm \(A,\,\,B,\,\,C,\,\,D\) cùng thuộc đường tròn tâm \(O\), bán kính \(R = OA = OB = OC = OD\).

Áp dụng định lí Pytago trong tam giác vuông \(ACD\) ta có:

\(AC = \sqrt {A{D^2} + C{D^2}}  = \sqrt {{{18}^2} + {{12}^2}}\)\(\,  = \sqrt {468}  = 6\sqrt {13} \,\,\left( {cm} \right)\).

Vậy \(R = OA = \dfrac{1}{2}AC = \dfrac{1}{2}.6\sqrt {13} \)\(\,  = 3\sqrt {13} \,\,\left( {cm} \right)\).

 Loigiaihay.com