Bài 73 trang 114 SBT Hình học 10 Nâng cao

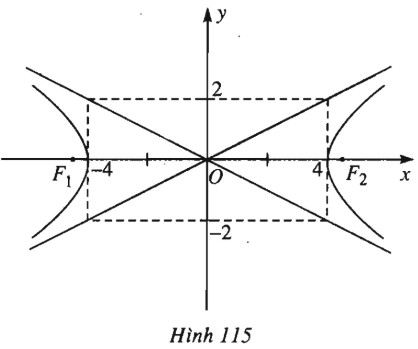
Đề bài

Xác định độ dài trục thực, trục ảo; tiêu cự; tâm sai; tọa độ các tiêu điểm, các đỉnh và phương trình các đường tiệm cận của mỗi hypebol có phương trình sau

a) \( \dfrac{{{x^2}}}{{16}} -  \dfrac{{{y^2}}}{4} = 1;\)                             

b) \(4{x^2} - {y^2} = 4;\)

c) \(16{x^2} - 25{y^2} = 400;\)

d) \(16{x^2} - 9{y^2} = 16;\)

e) \({x^2} - {y^2} = 1;\)

f) \(m{x^2} - n{y^2} = 1  (m > 0, n > 0).\)

Vẽ các hypebol có phương trình ở câu a), b) và e).

Lời giải chi tiết

a) \({a^2} = 16   \Rightarrow   a = 4 ; \) \( {b^2} = 4   \Rightarrow   b = 2; \) \( {c^2} = {a^2} + {b^2} = 20   \Rightarrow   c = 2\sqrt 5 \).

Độ dài trục thực : \(2a=8.\)

Độ dài trục ảo : \(2b=4.\)

Tiêu cự: \(2c = 4\sqrt 5 \), tâm sai \(e =  \dfrac{c}{a} =  \dfrac{{\sqrt 5 }}{2}\).

Các tiêu điểm : \({F_1}( - 2\sqrt 5  ; 0) ,  {F_2}(2\sqrt 5  ; 0)\)

Các đỉnh : \({A_1}( - 4 ; 0) , {A_2}(4 ; 0)\).

Các tiệm cận :  \(y =  \pm  \dfrac{b}{a}x =  \pm  \dfrac{1}{2}x\)

Hypebol được vẽ như hình 115.

b), c), d), e) làm tương tự.

f) Viết lại phương trình hypebol:

\(\begin{array}{l} \dfrac{{{x^2}}}{{ \dfrac{1}{m}}} -  \dfrac{{{y^2}}}{{ \dfrac{1}{n}}} = 1.\\{a^2} =  \dfrac{1}{m}    \Rightarrow   a =  \dfrac{1}{{\sqrt m }}  ,\\   {b^2} =  \dfrac{1}{n}    \Rightarrow    b =  \dfrac{1}{{\sqrt n }}.\\{c^2} = {a^2} + {b^2} =  \dfrac{1}{m} +  \dfrac{1}{n} \\  \Rightarrow   c = \sqrt { \dfrac{{m + n}}{{mn}}} .\end{array}\)

Độ dài trục thực : \(2a =  \dfrac{2}{{\sqrt m }}\) , độ dài trục ảo : \(2b =  \dfrac{2}{{\sqrt n }}\).

Tiêu cự : \(2c = 2\sqrt { \dfrac{{m + n}}{{mn}}} \).

Các tiêu điểm : \({F_1} = \left( { - \sqrt { \dfrac{{m + n}}{{mn}}}  ; 0} \right) ,\) \(  {F_2} = \left( {\sqrt { \dfrac{{m + n}}{{mn}}}  ; 0} \right)\).

Các đỉnh : \({A_1} = \left( { -  \dfrac{1}{{\sqrt m }} ; 0} \right) ,  {A_2} = \left( { \dfrac{1}{{\sqrt m }} ; 0} \right)\).

Các tiệm cận: \(y =  \pm \sqrt { \dfrac{m}{n}} .x\).

Loigiaihay.com