Bài 7.19 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức

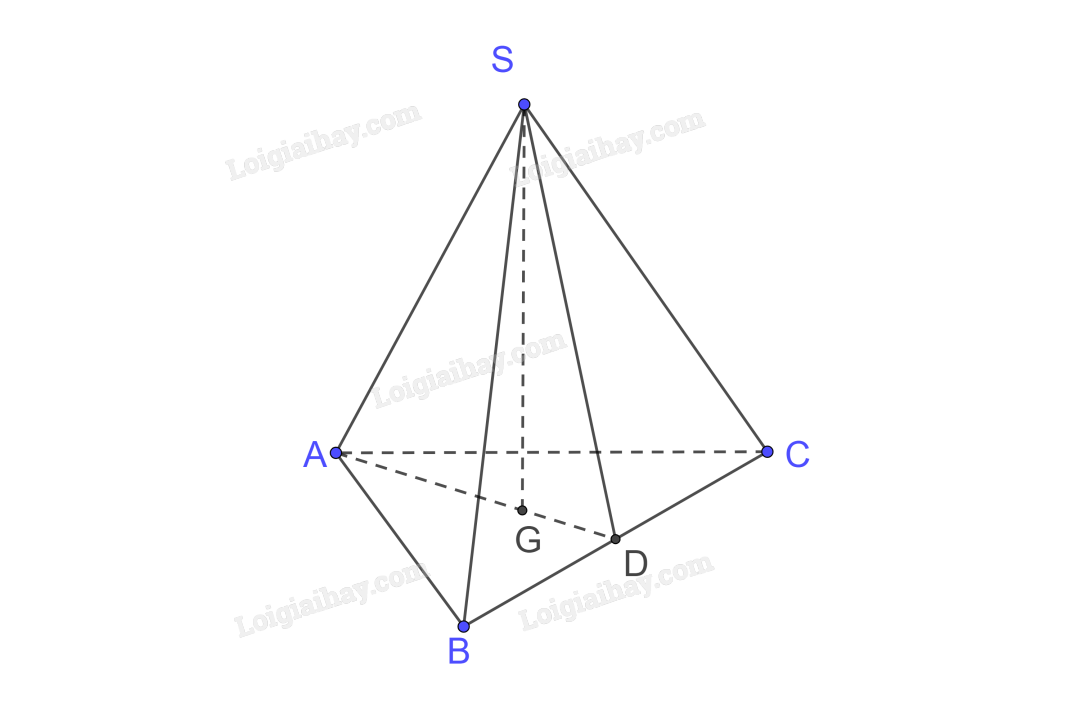
Đề bài

Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b.

a) Tính sin của góc tạo bởi cạnh bên và mặt đáy.

b) Tính tang của góc giữa mặt phẳng chứa mặt đáy và mặt phẳng chứa mặt bên.

Lời giải chi tiết

 

Vì hình chóp S.ABC đều, gọi G là hình chiếu của S trên (ABC) nên G là tâm của đáy ABC là tam giác đều do đó G cũng là trọng tâm hay trực tâm của tam giác ABC.

Gọi AG cắt BC tại D

a) Ta có A là hình chiếu của A trên (ABC)

G là hình chiếu của S trên (ABC)

\( \Rightarrow \) AG là hình chiếu của SA trên (ABC)

\( \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,AG} \right) = \widehat {SAG}\)

Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)

Mà G là trọng tâm nên \(AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)

Xét tam giác SAG vuông tại G có

\(SG = \sqrt {S{A^2} - A{G^2}}  = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}  = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)

\(\sin \widehat {SAG} = \frac{{SG}}{{SA}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :b = \sqrt {1 - \frac{{{a^2}}}{{3{b^2}}}} \)

b) Ta có \(AG \bot BC,SG \bot BC \Rightarrow BC \bot \left( {SAD} \right);SD \subset \left( {SAD} \right) \Rightarrow BC \bot SD\)

\(BC \bot AD\) (G là trực tâm)

\(\begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\ \Rightarrow \left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {AD,SD} \right) = \widehat {SDA}\end{array}\)

Mà G là trọng tâm nên \(GD = \frac{1}{3}AD = \frac{{a\sqrt 3 }}{6}\)

Xét tam giác SGD vuông tại G có

\(\tan \widehat {SGD} = \frac{{SG}}{{GD}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :\frac{{a\sqrt 3 }}{6} = \frac{6}{{a\sqrt 3 }}.\sqrt {{b^2} - \frac{{{a^2}}}{3}} \)