Bài 7 trang 140 SGK Đại số 10

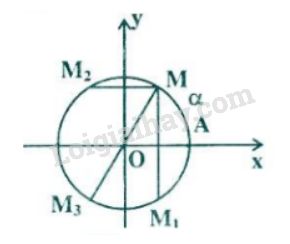
Đề bài

Trên đường tròn lượng giác cho điểm $M$ xác định bởi  $sđ\overparen{AM} = α \,  (0 < α < {\pi  \over 2}).$

Gọi $M_1, M_2, M_3$ lần lượt là điểm đối xứng của $M$ qua trục $Ox, Oy$ và gốc toạ độ. Tìm số đo các cung $\overparen{AM_1}, \,  \overparen{AM_2} , \, \overparen{AM_3}.$

Lời giải chi tiết

                         

Theo đề bài và hình vẽ ta có:

$sđ\overparen{AM_1} = – α + k2π$, $k\in\mathbb Z$ (vì $\overparen{AM_1}=\overparen{AM}$)

$sđ\overparen{AM_2} = π – α + l2π$, $l\in\mathbb Z$ (vì $\overparen{AM_2}=\pi -\alpha$)

$sđ\overparen{AM_3} = \pi + α + m2π$, $m\in\mathbb Z$ (vì $\overparen{AM_3}=\pi +\alpha$)

Loigiaihay.com