Bài 5 trang 140 SGK Đại số 10

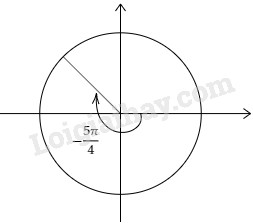
LG a

$\displaystyle - {{5\pi } \over 4}$;

Phương pháp giải:

+) Dựa vào lý thuyết mối liên hệ giữa các cung.

Lời giải chi tiết:

Trên hình bên. Cung có số đo $- \dfrac{{5\pi }}{4}$

Ta có:

$- \dfrac{{5\pi }}{4} = \dfrac{{ - 4\pi  - \pi }}{4}$$= \dfrac{{ - 4\pi }}{4} - \dfrac{\pi }{4}=  - \pi  - \dfrac{\pi }{4}$

Cách vẽ: Quay nửa vòng đường tròn cùng chiều kim đồng hồ rồi quay theo hướng đó thêm một nửa góc vuông nữa và dừng lại.

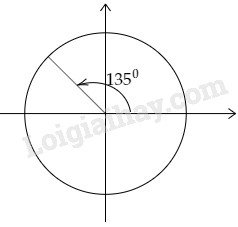
LG b

$\displaystyle 135^0$

Phương pháp giải:

+) Dựa vào lý thuyết mối liên hệ giữa các cung.

Lời giải chi tiết:

Nhận xét rằng ${135^0} = {90^0} + {45^0}$.

Cách vẽ: Ngược chiều kim đồng hồ quay một góc vuông và thêm nửa góc vuông nữa rồi dừng lại.

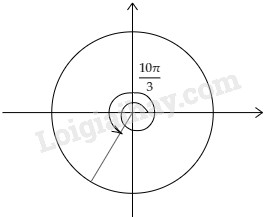
LG c

$\displaystyle {{10\pi } \over 3}$;

Phương pháp giải:

+) Dựa vào lý thuyết mối liên hệ giữa các cung.

Lời giải chi tiết:

Vẽ cung $\dfrac{10 \pi}{3}.$

Ta có:

$\dfrac{{10\pi }}{3}  = \dfrac{{9\pi  + \pi }}{3} = \dfrac{{9\pi }}{3} + \dfrac{\pi }{3}$$= 3\pi  + \dfrac{\pi }{3}= 2\pi  + \pi  + \dfrac{\pi }{3}$

Cách vẽ:

Đi theo chiều dương kể từ A, vẽ một vòng tròn, thêm một nửa vòng tròn nữa ta được cung $3\pi$, vẽ thêm một phần ba của nửa vòng tròn rồi dừng lại ta được cung $\dfrac{10 \pi}{3}.$

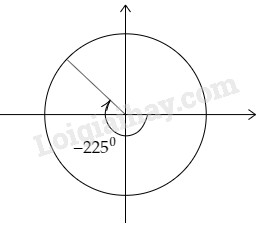
LG d

$\displaystyle -225^0$ 

Phương pháp giải:

+) Dựa vào lý thuyết mối liên hệ giữa các cung.

Lời giải chi tiết:

Ta có: $- {225^0} =  - {180^0} - {45^0}$.

Cách vẽ: Quay nửa vòng đường tròn cùng chiều kim đồng hồ rồi quay theo hướng đó thêm một nửa góc vuông nữa và dừng lại.

Loigiaihay.com