Bài 7 trang 127 SGK Hình học 10 nâng caoTính khoảng cách từ gốc tọa độ O tới đường thẳng M1M2 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Trong mặt phẳng tọa độ, với mỗi số \(m \ne 0\) , xét hai điểm \({M_1}( - 4\,;\,m);\,{M_2}(4\,;\,{{16} \over m})\) LG a Viết phương trình đường thẳng M1M2. Lời giải chi tiết: Ta có \(\overrightarrow {{M_1}{M_2}} = \left( {8\,;\,{{16} \over m} - m} \right) = \left( {8\,;\,{{16 - {m^2}} \over m}} \right)\) \( \Rightarrow \overrightarrow n = \left( {\frac{{16 - {m^2}}}{m}; - 8} \right)\) là VTPT của đường thẳng \({M_1}{M_2}\). Phương trình đường thẳng \({M_1}{M_2}\) đi qua \(M_1\) và nhận \(\overrightarrow n = \left( {\frac{{16 - {m^2}}}{m}; - 8} \right)\) làm VTPT là: \(\begin{array}{l} LG b Tính khoảng cách từ gốc tọa độ O tới đường thẳng M1M2. Lời giải chi tiết: Khoảng cách từ O đến đường thẳng M1M2 là \(\begin{array}{l} LG c Chứng tỏ rằng đường thẳng M1M2 luôn tiếp xúc với một đường tròn cố định. Lời giải chi tiết: * Gọi ( C) là đường tròn tâm O, bán kính R = 4. => Đường tròn (C) cố định. * Theo chứng minh b ta có: d(O, M1M2) = 4 = R – không phụ thuộc vào m. => Đường thẳng M1M2 luôn tiếp xúc với đường tròn (C) cố định. LG d Lấy các điểm \({A_1}( - 4;\,0),\,{A_2}(4\,;\,0)\). Tìm tọa độ giao điểm I của hai đường thẳng \({A_1}{M_2},\,{A_2}{M_1}\) . Lời giải chi tiết: Phương trình đường thẳng A1M2 là \({{x + 4} \over 8} = {{y - 0} \over {{{16} \over m}}}\,\,\, \Leftrightarrow \,\,\,2x - my + 8 = 0\) Phương trình đường thẳng A2M1 là \({{x - 4} \over { - 8}} = {{y - 0} \over m}\,\,\,\, \Leftrightarrow \,\,\,mx + 8y - 4m = 0\) Tọa độ giao điểm I của A1M2 và A2M1 là nghiệm của hệ phương trình
Vậy \(I\left( {{{4({m^2} - 16)} \over {{m^2} + 16}}\,;\,{{16m} \over {{m^2} + 16}}} \right)\) . LG e Chứng minh rằng khi m thay đổi, I luôn luôn nằm trên một elip (E) cố định. Xác định tọa độ tiêu điểm của elip đó. Lời giải chi tiết: Khử m từ hệ (*) ta có \(\eqalign{ Vậy I nằm trên elip (E) có phương trình \(\,\,{{{x^2}} \over {16}} + {{{y^2}} \over 4} = 1\) . Ta có \({c^2} = {a^2} - {b^2} = 16 - 4 = 12\) \( \Rightarrow \,\,c = 2\sqrt 3 \) Hai tiêu điểm của elip là \({F_1}( - 2\sqrt 3 \,;\,0)\,,\,\,\,{F_2}(2\sqrt 3 \,;\,0)\) Loigiaihay.com
|














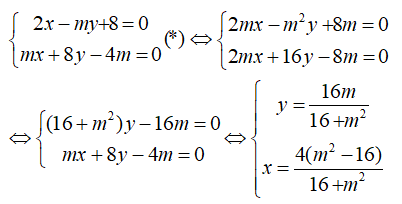






Danh sách bình luận